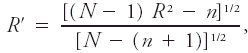Multiple correlation: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot No edit summary |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">The [[correlation]] between a [[random variable]] and its [[regression function]].</div><br/> <div class="paragraph">If ''Y'' denotes the regression function of a random variable ([[variate]]) ''y'' with respect to certain other variates ''x''<sub>1</sub>, ''x''<sub>2</sub> . . ., ''x''<sub>''n''</sub> then the [[coefficient of multiple correlation]] between ''y'' and the ''x'''s is defined as the coefficient of simple, [[linear correlation]] between ''y'' and ''Y''. However, the constants of the regression function automatically adjust for algebraic sign, with the result that the [[coefficient of correlation]] between ''y'' and ''Y'' cannot be negative; in fact, its value is precisely equal to the ratio of their two [[standard deviations]], that is, σ(''Y'')/σ(''y''). Therefore, the coefficient of multiple correlation ranges from 0 to 1, and the square of the coefficient of multiple correlation is equal to the [[relative reduction]] (or [[percent reduction]]), that is, the ratio of [[explained variance]] to [[total variance]]. Since, in practice, the true regression function ''Y'' is seldom known, it is ordinarily necessary to hypothesize its mathematical form and determine the constants by [[least squares]], thus obtaining the approximation ''Y''′. In that case, the conventional estimate of the multiple correlation is the [[sample]] value of the simple linear correlation (symbol ''R'') between ''y'' and ''Y''′, although a better estimate is obtained by incorporating a correction for [[degrees of freedom]]. Such a corrected value ''R''′ is given as follows: <div class="display-formula"><blockquote>[[File:ams2001glos-Me35.gif|link=|center|ams2001glos-Me35]]</blockquote></div> where ''N'' denotes the sample size and ''n'' + 1 equals the total number of constants (including the [[absolute]] term) determined from the data. In case (''N'' - 1) ''R''<sup>2</sup> < ''n'', the value of ''R''′ is taken as zero. <br/>''See'' [[regression]].</div><br/> </div> | <div class="definition"><div class="short_definition">The [[correlation]] between a [[random variable]] and its [[regression function]].</div><br/> <div class="paragraph">If ''Y'' denotes the regression function of a random variable ([[variate]]) ''y'' with respect to certain other variates ''x''<sub>1</sub>, ''x''<sub>2</sub> . . ., ''x''<sub>''n''</sub> then the [[coefficient of multiple correlation]] between ''y'' and the ''x'''s is defined as the coefficient of simple, [[linear correlation]] between ''y'' and ''Y''. However, the constants of the regression function automatically adjust for algebraic sign, with the result that the [[coefficient of correlation|coefficient of correlation]] between ''y'' and ''Y'' cannot be negative; in fact, its value is precisely equal to the ratio of their two [[standard deviations]], that is, σ(''Y'')/σ(''y''). Therefore, the coefficient of multiple correlation ranges from 0 to 1, and the square of the coefficient of multiple correlation is equal to the [[relative reduction]] (or [[percent reduction]]), that is, the ratio of [[explained variance]] to [[total variance|total variance]]. Since, in practice, the true regression function ''Y'' is seldom known, it is ordinarily necessary to hypothesize its mathematical form and determine the constants by [[least squares]], thus obtaining the approximation ''Y''′. In that case, the conventional estimate of the multiple correlation is the [[sample]] value of the simple linear correlation (symbol ''R'') between ''y'' and ''Y''′, although a better estimate is obtained by incorporating a correction for [[degrees of freedom]]. Such a corrected value ''R''′ is given as follows: <div class="display-formula"><blockquote>[[File:ams2001glos-Me35.gif|link=|center|ams2001glos-Me35]]</blockquote></div> where ''N'' denotes the sample size and ''n'' + 1 equals the total number of constants (including the [[absolute]] term) determined from the data. In case (''N'' - 1) ''R''<sup>2</sup> < ''n'', the value of ''R''′ is taken as zero. <br/>''See'' [[regression]].</div><br/> </div> | ||
</div> | </div> | ||
Latest revision as of 16:28, 25 April 2012
multiple correlation
If Y denotes the regression function of a random variable (variate) y with respect to certain other variates x1, x2 . . ., xn then the coefficient of multiple correlation between y and the x's is defined as the coefficient of simple, linear correlation between y and Y. However, the constants of the regression function automatically adjust for algebraic sign, with the result that the coefficient of correlation between y and Y cannot be negative; in fact, its value is precisely equal to the ratio of their two standard deviations, that is, σ(Y)/σ(y). Therefore, the coefficient of multiple correlation ranges from 0 to 1, and the square of the coefficient of multiple correlation is equal to the relative reduction (or percent reduction), that is, the ratio of explained variance to total variance. Since, in practice, the true regression function Y is seldom known, it is ordinarily necessary to hypothesize its mathematical form and determine the constants by least squares, thus obtaining the approximation Y′. In that case, the conventional estimate of the multiple correlation is the sample value of the simple linear correlation (symbol R) between y and Y′, although a better estimate is obtained by incorporating a correction for degrees of freedom. Such a corrected value R′ is given as follows: where N denotes the sample size and n + 1 equals the total number of constants (including the absolute term) determined from the data. In case (N - 1) R2 < n, the value of R′ is taken as zero.
See regression.
See regression.