Correlation coefficient: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == correlation coefficient == </div> #<div class="definition"><div class="short_definition"><b...") |
imported>Perlwikibot No edit summary |
||
| Line 10: | Line 10: | ||
#<div class="definition"><div class="short_definition"><br/>''See'' [[correlation]].</div><br/> </div> | #<div class="definition"><div class="short_definition"><br/>''See'' [[correlation]].</div><br/> </div> | ||
#<div class="definition"><div class="short_definition">A measure of the [[persistence]] of the [[eddy velocity]] as a function of time and space.</div><br/> <div class="paragraph">Two types are distinguished: 1) In the [[Eulerian correlation]] coefficient, the time difference is zero, <div class="display-formula"><blockquote>[[File:ams2001glos-Ce43.gif|link=|center|ams2001glos-Ce43]]</blockquote></div> where ''u''′ is the eddy velocity. For [[homogeneous]] and [[homologous turbulence]], this [[correlation]] tensor depends only on the difference (''y''<sub>2</sub> | #<div class="definition"><div class="short_definition">A measure of the [[persistence]] of the [[eddy velocity]] as a function of time and space.</div><br/> <div class="paragraph">Two types are distinguished: 1) In the [[Eulerian correlation]] coefficient, the time difference is zero, <div class="display-formula"><blockquote>[[File:ams2001glos-Ce43.gif|link=|center|ams2001glos-Ce43]]</blockquote></div> where ''u''′ is the eddy velocity. For [[homogeneous]] and [[homologous turbulence]], this [[correlation]] tensor depends only on the difference (''y''<sub>2</sub> - ''y''<sub>1</sub>); when the [[turbulence]] is [[isotropic]], the [[tensor]] is spherically symmetric and <div class="inline-formula">[[File:ams2001glos-Cex10.gif|link=|ams2001glos-Cex10]]</div>. 2) In the [[Lagrangian correlation]] coefficient, time and space are varied together in such a way that the same [[fluid parcel]] is being followed: <div class="display-formula"><blockquote>[[File:ams2001glos-Ce44.gif|link=|center|ams2001glos-Ce44]]</blockquote></div> When the flow is one-dimensional and the [[mean velocity]] is much greater than the [[eddy velocity]], then a fixed point experiences approximately the same sequence of fluctuations as a fluid parcel. The Lagrangian correlation coefficient can then be converted into the Eulerian by a proper scaling. These correlation coefficients have the same form and meaning when any other fluctuating quantity is used, for example, [[temperature]] or [[pressure]].</div><br/> </div> | ||
</div> | </div> | ||
Revision as of 13:59, 20 February 2012
correlation coefficient
See correlation.
- A measure of the persistence of the eddy velocity as a function of time and space.
Two types are distinguished: 1) In the Eulerian correlation coefficient, the time difference is zero,where u′ is the eddy velocity. For homogeneous and homologous turbulence, this correlation tensor depends only on the difference (y2 - y1); when the turbulence is isotropic, the tensor is spherically symmetric and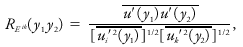
. 2) In the Lagrangian correlation coefficient, time and space are varied together in such a way that the same fluid parcel is being followed:
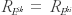When the flow is one-dimensional and the mean velocity is much greater than the eddy velocity, then a fixed point experiences approximately the same sequence of fluctuations as a fluid parcel. The Lagrangian correlation coefficient can then be converted into the Eulerian by a proper scaling. These correlation coefficients have the same form and meaning when any other fluctuating quantity is used, for example, temperature or pressure.
