Froude number

Froude number

1. The nondimensional ratio of the inertial force to the force of gravity for a given fluid flow; the reciprocal of the Reech number.

   
   

   It may be given as

   

   where V is a characteristic velocity, L a characteristic length, and g the acceleration of gravity; or as the square root of this number.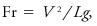

   
   
2. For atmospheric flows over hills or other obstacles, a more useful form of the Froude number is

   

   where N_BV is the Brunt–Väisälä frequency of the ambient upstream environment, V is the wind speed component across the mountain, and L_w is the width of the mountain.

   
   

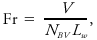
   Fr can be interpreted as the ratio of natural wavelength of the air to wavelength of the mountain. Sometimes π will appear in the numerator, and other times the ratio will be squared. When Fr = 1, the natural wavelength of the air is in resonance with the size of the mountain and creates the most intense mountain waves, which can sometimes contain lenticular clouds and rotors of reverse flow at the surface. For Fr < 1, some of the low-altitude upstream air is blocked by the hill, short-wavelength waves separate from the top of the hill, and the remaining air at lower altitudes flows laterally around the hill. For Fr > 1, very long wavelengths form downwind of the hill, and can include a cavity of reverse flow just to the lee of the hill near the surface. Another form of the Froude number, using (z_i − z_hill) in place of L_w, is useful for diagnosing downslope windstorms and hydraulic jump, where z_i is the depth of the mixed layer above the base of the mountain, and z_hill is the height of the mountain.

   
   

• INDEX
• A
• B
• C
• D
• E
• F
• G
• H
• I
• J
• K
• L
• M
• N
• O
• P
• Q
• R
• S
• T
• U
• V
• W
• X
• Y
• Z
• 0
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9

1. A measure (or condition) of height, especially of great height, as a mountain top or aircraft flight level.