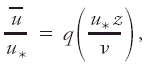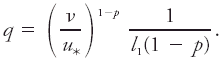Power-law profile: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == power-law profile == </div> <div class="definition"><div class="short_definition">A formula...") |
imported>Perlwikibot No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">A formula for the [[variation]] of [[wind]] with height in the [[surface boundary layer]].</div><br/> <div class="paragraph">It is an alternative to the [[logarithmic velocity profile]], and the assumptions are the same, with the exception of the form of the dependence of [[mixing length]] ''l'' on height ''z''. Here <div class="display-formula"><blockquote>[[File:ams2001glos-Pe44.gif|link=|center|ams2001glos-Pe44]]</blockquote></div> Then <div class="display-formula"><blockquote>[[File:ams2001glos-Pe45.gif|link=|center|ams2001glos-Pe45]]</blockquote></div> where <div class="inline-formula">[[File:ams2001glos-Pex07.gif|link=|ams2001glos-Pex07]]</div> is the [[mean velocity]], ''u''<sub>*</sub> the [[friction velocity]], ν the [[kinematic viscosity]], and <div class="display-formula"><blockquote>[[File:ams2001glos-Pe46.gif|link=|center|ams2001glos-Pe46]]</blockquote></div> For moderate [[Reynolds numbers]], ''p'' = 6/7 (the seventh-root profile) is empirically verified, but for large Reynolds numbers ''p'' is between this value and unity. It is to be noted that if <div class="inline-formula">[[File:ams2001glos-Pex08.gif|link=|ams2001glos-Pex08]]</div> is proportional to ''z''<sup>''m''</sup>, and if the [[stress]] is assumed independent of height, then the [[eddy viscosity]] ν<sub>''e''</sub> is proportional to ''z''<sup>1 | <div class="definition"><div class="short_definition">A formula for the [[variation]] of [[wind]] with height in the [[surface boundary layer]].</div><br/> <div class="paragraph">It is an alternative to the [[logarithmic velocity profile]], and the assumptions are the same, with the exception of the form of the dependence of [[mixing length]] ''l'' on height ''z''. Here <div class="display-formula"><blockquote>[[File:ams2001glos-Pe44.gif|link=|center|ams2001glos-Pe44]]</blockquote></div> Then <div class="display-formula"><blockquote>[[File:ams2001glos-Pe45.gif|link=|center|ams2001glos-Pe45]]</blockquote></div> where <div class="inline-formula">[[File:ams2001glos-Pex07.gif|link=|ams2001glos-Pex07]]</div> is the [[mean velocity]], ''u''<sub>*</sub> the [[friction velocity]], ν the [[kinematic viscosity|kinematic viscosity]], and <div class="display-formula"><blockquote>[[File:ams2001glos-Pe46.gif|link=|center|ams2001glos-Pe46]]</blockquote></div> For moderate [[Reynolds numbers]], ''p'' = 6/7 (the seventh-root profile) is empirically verified, but for large Reynolds numbers ''p'' is between this value and unity. It is to be noted that if <div class="inline-formula">[[File:ams2001glos-Pex08.gif|link=|ams2001glos-Pex08]]</div> is proportional to ''z''<sup>''m''</sup>, and if the [[stress]] is assumed independent of height, then the [[eddy viscosity]] ν<sub>''e''</sub> is proportional to ''z''<sup>1-''m''</sup>. These relations are known as Schmidt's conjugate-power laws.</div><br/> </div><div class="reference">Sutton, O. G. 1953. Micrometeorology. 78–85. </div><br/> | ||
</div> | </div> | ||
Latest revision as of 16:39, 25 April 2012
power-law profile
It is an alternative to the logarithmic velocity profile, and the assumptions are the same, with the exception of the form of the dependence of mixing length l on height z. Here Then where 
is the mean velocity, u* the friction velocity, ν the kinematic viscosity, and For moderate Reynolds numbers, p = 6/7 (the seventh-root profile) is empirically verified, but for large Reynolds numbers p is between this value and unity. It is to be noted that if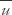 
is proportional to zm, and if the stress is assumed independent of height, then the eddy viscosity νe is proportional to z1-m. These relations are known as Schmidt's conjugate-power laws.
Sutton, O. G. 1953. Micrometeorology. 78–85.
