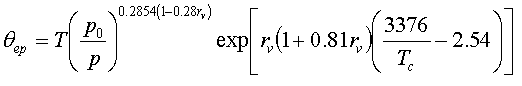Pseudoequivalent potential temperature: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == pseudoequivalent potential temperature == </div> <div class="definition"><div class="short_...") |
imported>Liss45 |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">The [[temperature]] a sample of air would have if it were expanded by a [[pseudoadiabatic process]] to zero [[pressure]] and then compressed to a reference pressure of | <div class="definition"><div class="short_definition">The [[temperature]] a sample of air would have if it were expanded by a [[pseudoadiabatic process]] to zero [[pressure]] and then compressed to a reference pressure of 1000 hPa by a [[dry-adiabatic process]].</div><br/> <div class="paragraph">This quantity is conserved in a pseudoadiabatic process and is given approximately by <div class="display-formula"><blockquote>[[File:ams2001glos-Pe59.gif|link=|center|ams2001glos-Pe59]]</blockquote></div> where ''T'' is the temperature, ''p'' is the pressure, ''T''<sub>''c''</sub> is the [[condensation temperature]] (obtainable from the [[dewpoint formula]]) and ''r''<sub>''v''</sub> is the [[water vapor]] mixing ratio. When ''r''<sub>''v''</sub> = 0, θ<sub>''ep''</sub> = θ, the [[potential temperature]].</div><br/> </div><div class="reference">Bolton, D. 1980. The computation of equivalent potential temperature. Mon. Wea. Rev.. 108. 1046–1053. </div><br/> | ||
</div> | </div> | ||
Revision as of 13:11, 1 May 2013
pseudoequivalent potential temperature
The temperature a sample of air would have if it were expanded by a pseudoadiabatic process to zero pressure and then compressed to a reference pressure of 1000 hPa by a dry-adiabatic process.
This quantity is conserved in a pseudoadiabatic process and is given approximately by where T is the temperature, p is the pressure, Tc is the condensation temperature (obtainable from the dewpoint formula) and rv is the water vapor mixing ratio. When rv = 0, θep = θ, the potential temperature.
Bolton, D. 1980. The computation of equivalent potential temperature. Mon. Wea. Rev.. 108. 1046–1053.