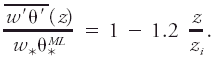Mixed-layer similarity: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == mixed-layer similarity == </div> <div class="definition"><div class="short_definition">An e...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">An empirical method of finding universal relationships between [[boundary layer]] variables that are made dimensionless using the [[Deardorff velocity]] ''w''<sub>*</sub>, the [[mixed-layer depth]] ''z''<sub>''i''</sub>, and the mixed-layer [[temperature scale]] <div class="inline-formula">[[File:ams2001glos-Mex01.gif|link=|ams2001glos-Mex01]]</div>, where <div class="inline-formula">[[File:ams2001glos-Mex02.gif|link=|ams2001glos-Mex02]]</div> is the surface kinematic [[heat flux]].</div><br/> <div class="paragraph">The resulting universal relationships are valid only for convective [[mixed layers]]. An example is <div class="display-formula"><blockquote>[[File:ams2001glos-Me11.gif|link=|center|ams2001glos-Me11]]</blockquote></div><br/>''Compare'' [[local free-convection similarity]], [[local similarity]], [[similarity theory]], [[dimensional analysis]], [[Buckingham Pi theory]].</div><br/> </div><div class="reference">Stull, R. B. 1988. An Introduction to Boundary Layer Meteorology. 666 pp. </div><br/> | <div class="definition"><div class="short_definition">An empirical method of finding universal relationships between [[boundary layer|boundary layer]] variables that are made dimensionless using the [[Deardorff velocity]] ''w''<sub>*</sub>, the [[mixed-layer depth|mixed-layer depth]] ''z''<sub>''i''</sub>, and the mixed-layer [[temperature scale]] <div class="inline-formula">[[File:ams2001glos-Mex01.gif|link=|ams2001glos-Mex01]]</div>, where <div class="inline-formula">[[File:ams2001glos-Mex02.gif|link=|ams2001glos-Mex02]]</div> is the surface kinematic [[heat flux]].</div><br/> <div class="paragraph">The resulting universal relationships are valid only for convective [[mixed layers]]. An example is <div class="display-formula"><blockquote>[[File:ams2001glos-Me11.gif|link=|center|ams2001glos-Me11]]</blockquote></div><br/>''Compare'' [[local free-convection similarity]], [[local similarity]], [[similarity theory]], [[dimensional analysis]], [[Buckingham Pi theory]].</div><br/> </div><div class="reference">Stull, R. B. 1988. An Introduction to Boundary Layer Meteorology. 666 pp. </div><br/> | ||
</div> | </div> | ||
Latest revision as of 16:26, 25 April 2012
mixed-layer similarity
An empirical method of finding universal relationships between boundary layer variables that are made dimensionless using the Deardorff velocity w*, the mixed-layer depth zi, and the mixed-layer temperature scale 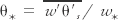 , where
, where 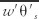 is the surface kinematic heat flux.
is the surface kinematic heat flux.
The resulting universal relationships are valid only for convective mixed layers. An example is
Compare local free-convection similarity, local similarity, similarity theory, dimensional analysis, Buckingham Pi theory.
Compare local free-convection similarity, local similarity, similarity theory, dimensional analysis, Buckingham Pi theory.
Stull, R. B. 1988. An Introduction to Boundary Layer Meteorology. 666 pp.