Mixing length: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == mixing length == </div> #<div class="definition"><div class="short_definition">An average d...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
#<div class="definition"><div class="short_definition">An average distance of [[air parcel]] turbulent movement toward a reference height, where the average is a root-mean-square distance.</div><br/> <div class="paragraph">It is also known as Prandtl's mixing length, ''l'', after Ludwig Prandtl who devised it in 1925 to explain [[turbulent fluxes]] such as the [[Reynolds stress]], τ. Prandtl started with Boussinesq's [[first- order turbulence closure]] hypothesis that <div class="inline-formula">[[File:ams2001glos-Mex03.gif|link=|ams2001glos-Mex03]]</div>, where ρ is [[density]], <div class="inline-formula">[[File:ams2001glos-Mex04.gif|link=|ams2001glos-Mex04]]</div> is average horizontal [[velocity]], and Κ is kinematic [[eddy viscosity]]. He further recognized that [[exchange coefficient]] Κ has units of length times velocity, and proposed that Κ = ''l''''w'', where ''w'' is a representative average turbulent vertical velocity. Prandtl also suggested that turbulent vertical motions are caused by the collision of air parcels moving horizontally at different speeds. This results in turbulent vertical velocity being proportional to turbulent horizontal velocity. From this, it can be shown that eddy viscosity can be approximated by <div class="inline-formula">[[File:ams2001glos-Mex05.gif|link=|ams2001glos-Mex05]]</div>, which can be used in Boussinesq's first-order closure.</div><br/> </div> | #<div class="definition"><div class="short_definition">An average distance of [[air parcel]] turbulent movement toward a reference height, where the average is a root-mean-square distance.</div><br/> <div class="paragraph">It is also known as Prandtl's mixing length, ''l'', after Ludwig Prandtl who devised it in 1925 to explain [[turbulent flux|turbulent fluxes]] such as the [[Reynolds stresses|Reynolds stress]], τ. Prandtl started with Boussinesq's [[first-order closure|first- order turbulence closure]] hypothesis that <div class="inline-formula">[[File:ams2001glos-Mex03.gif|link=|ams2001glos-Mex03]]</div>, where ρ is [[density]], <div class="inline-formula">[[File:ams2001glos-Mex04.gif|link=|ams2001glos-Mex04]]</div> is average horizontal [[velocity]], and Κ is kinematic [[eddy viscosity]]. He further recognized that [[exchange coefficients|exchange coefficient]] Κ has units of length times velocity, and proposed that Κ = ''l''''w'', where ''w'' is a representative average turbulent vertical velocity. Prandtl also suggested that turbulent vertical motions are caused by the collision of air parcels moving horizontally at different speeds. This results in turbulent vertical velocity being proportional to turbulent horizontal velocity. From this, it can be shown that eddy viscosity can be approximated by <div class="inline-formula">[[File:ams2001glos-Mex05.gif|link=|ams2001glos-Mex05]]</div>, which can be used in Boussinesq's first-order closure.</div><br/> </div> | ||
#<div class="definition"><div class="short_definition">A mean length of travel over which an [[air parcel]] maintains its identity before being mixed with the surrounding fluid; analogous to the [[mean free path]] of a molecule.</div><br/> </div><div class="reference">Stull, R. B. 1988. An Introduction to Boundary Layer Meteorology. 666 pp. </div><br/> | #<div class="definition"><div class="short_definition">A mean length of travel over which an [[air parcel]] maintains its identity before being mixed with the surrounding fluid; analogous to the [[mean free path]] of a molecule.</div><br/> </div><div class="reference">Stull, R. B. 1988. An Introduction to Boundary Layer Meteorology. 666 pp. </div><br/> | ||
</div> | </div> | ||
Latest revision as of 16:26, 25 April 2012
mixing length
- An average distance of air parcel turbulent movement toward a reference height, where the average is a root-mean-square distance.
It is also known as Prandtl's mixing length, l, after Ludwig Prandtl who devised it in 1925 to explain turbulent fluxes such as the Reynolds stress, τ. Prandtl started with Boussinesq's first- order turbulence closure hypothesis that, where ρ is density,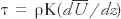
is average horizontal velocity, and Κ is kinematic eddy viscosity. He further recognized that exchange coefficient Κ has units of length times velocity, and proposed that Κ = l'w, where w is a representative average turbulent vertical velocity. Prandtl also suggested that turbulent vertical motions are caused by the collision of air parcels moving horizontally at different speeds. This results in turbulent vertical velocity being proportional to turbulent horizontal velocity. From this, it can be shown that eddy viscosity can be approximated by
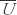, which can be used in Boussinesq's first-order closure.
- A mean length of travel over which an air parcel maintains its identity before being mixed with the surrounding fluid; analogous to the mean free path of a molecule.
Stull, R. B. 1988. An Introduction to Boundary Layer Meteorology. 666 pp.
