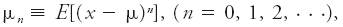Moment: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot No edit summary |
imported>Perlwikibot No edit summary |
||
| Line 10: | Line 10: | ||
#<div class="definition"><div class="short_definition">The product of a distance and another [[parameter]].</div><br/> <div class="paragraph">The moment may be about a point, line, or plane; if the parameter is a [[vector]], the moment is the [[vector product]] of the vector distance from the point, line, or plane, into the parameter. Thus, the moment of the [[momentum]] of a [[fluid parcel]] per unit volume about an axis is '''r''' × ρ'''u''', where '''r''' is the vector from axis to the parcel, ρ the [[density]], and '''u''' the [[velocity]] vector of the parcel; this is also called the [[angular momentum]]. The moment of a force '''F''' about an axis is '''r''' × '''F''', called the [[torque]]. The second moment of a parameter is the moment of the first moment, and so on, for higher moments.</div><br/> </div> | #<div class="definition"><div class="short_definition">The product of a distance and another [[parameter]].</div><br/> <div class="paragraph">The moment may be about a point, line, or plane; if the parameter is a [[vector]], the moment is the [[vector product]] of the vector distance from the point, line, or plane, into the parameter. Thus, the moment of the [[momentum]] of a [[fluid parcel]] per unit volume about an axis is '''r''' × ρ'''u''', where '''r''' is the vector from axis to the parcel, ρ the [[density]], and '''u''' the [[velocity]] vector of the parcel; this is also called the [[angular momentum]]. The moment of a force '''F''' about an axis is '''r''' × '''F''', called the [[torque]]. The second moment of a parameter is the moment of the first moment, and so on, for higher moments.</div><br/> </div> | ||
#<div class="definition"><div class="short_definition">By analogy, in [[statistical]] terminology, the [[mean value]] of a power of a [[random variable]].</div><br/> <div class="paragraph">The symbol μ<sub>''n''</sub>′ (or ν<sub>''n''</sub>) is used for a [[raw moment]] as distinguished from the corresponding [[central moment]] μ<sub>''n''</sub> taken about the mean μ. Thus the raw moments are <div class="display-formula"><blockquote>[[File:ams2001glos-Me24.gif|link=|center|ams2001glos-Me24]]</blockquote></div> where ''E''(''x''<sup>''n''</sup>) is the [[expected value]] of the [[variate]] ''x'' to the ''n''th power. In particular, μ<sub>0</sub>′ ≡ 1 and μ<sub>1</sub>′ ≡ ν<sub>1</sub> ≡ μ. The central moments are <div class="display-formula"><blockquote>[[File:ams2001glos-Me25.gif|link=|center|ams2001glos-Me25]]</blockquote></div> where ''E''[(''x'' - μ)<sup>''n''</sup>] is the expected value of the ''n''th power of the [[deviation]] of the variate from its mean. In particular, μ<sub>0</sub> ≡ 1, μ<sub>1</sub> ≡ 0, μ<sub>2</sub> ≡ σ<sup>2</sup>, where σ<sup>2</sup> is the [[variance]].</div><br/> </div> | #<div class="definition"><div class="short_definition">By analogy, in [[statistical]] terminology, the [[mean value|mean value]] of a power of a [[random variable]].</div><br/> <div class="paragraph">The symbol μ<sub>''n''</sub>′ (or ν<sub>''n''</sub>) is used for a [[raw moment]] as distinguished from the corresponding [[central moment]] μ<sub>''n''</sub> taken about the mean μ. Thus the raw moments are <div class="display-formula"><blockquote>[[File:ams2001glos-Me24.gif|link=|center|ams2001glos-Me24]]</blockquote></div> where ''E''(''x''<sup>''n''</sup>) is the [[expected value]] of the [[variate]] ''x'' to the ''n''th power. In particular, μ<sub>0</sub>′ ≡ 1 and μ<sub>1</sub>′ ≡ ν<sub>1</sub> ≡ μ. The central moments are <div class="display-formula"><blockquote>[[File:ams2001glos-Me25.gif|link=|center|ams2001glos-Me25]]</blockquote></div> where ''E''[(''x'' - μ)<sup>''n''</sup>] is the expected value of the ''n''th power of the [[deviation]] of the variate from its mean. In particular, μ<sub>0</sub> ≡ 1, μ<sub>1</sub> ≡ 0, μ<sub>2</sub> ≡ σ<sup>2</sup>, where σ<sup>2</sup> is the [[variance]].</div><br/> </div> | ||
</div> | </div> | ||
Latest revision as of 16:27, 25 April 2012
moment
- The product of a distance and another parameter.
The moment may be about a point, line, or plane; if the parameter is a vector, the moment is the vector product of the vector distance from the point, line, or plane, into the parameter. Thus, the moment of the momentum of a fluid parcel per unit volume about an axis is r × ρu, where r is the vector from axis to the parcel, ρ the density, and u the velocity vector of the parcel; this is also called the angular momentum. The moment of a force F about an axis is r × F, called the torque. The second moment of a parameter is the moment of the first moment, and so on, for higher moments.
The symbol μn′ (or νn) is used for a raw moment as distinguished from the corresponding central moment μn taken about the mean μ. Thus the raw moments arewhere E(xn) is the expected value of the variate x to the nth power. In particular, μ0′ ≡ 1 and μ1′ ≡ ν1 ≡ μ. The central moments are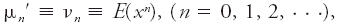
where E[(x - μ)n] is the expected value of the nth power of the deviation of the variate from its mean. In particular, μ0 ≡ 1, μ1 ≡ 0, μ2 ≡ σ2, where σ2 is the variance.
