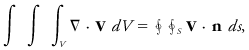Divergence theorem: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == divergence theorem == </div> <div class="definition"><div class="short_definition">(<br/>''...") |
imported>Perlwikibot No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">( | <div class="definition"><div class="short_definition">(''Also called'' Gauss's theorem.) The statement that the volume integral of the [[divergence]] of a [[vector]], such as the [[velocity]] '''V''', over a volume ''V'' is equal to the [[surface integral]] of the normal component of '''V''' over the surface ''s'' of the volume (often called the "export" through the closed surface), provided that '''V''' and its derivatives are continuous and single-valued throughout ''V'' and ''s''.</div><br/> <div class="paragraph">This may be written <div class="display-formula"><blockquote>[[File:ams2001glos-De37.gif|link=|center|ams2001glos-De37]]</blockquote></div> where '''n''' is a unit [[vector]] normal to the element of surface ''ds'', and the symbol ∮ ∮<sub>''S''</sub> indicates that the integration is to be carried out over a closed surface. This theorem is sometimes called [[Green's theorem|Green's theorem]] in the plane for the case of two-dimensional flow, and Green's theorem in space for the three-dimensional case described above. The divergence theorem is used extensively in manipulating the meteorological [[equations of motion]].</div><br/> </div> | ||
</div> | </div> | ||
Latest revision as of 15:49, 25 April 2012
divergence theorem
(Also called Gauss's theorem.) The statement that the volume integral of the divergence of a vector, such as the velocity V, over a volume V is equal to the surface integral of the normal component of V over the surface s of the volume (often called the "export" through the closed surface), provided that V and its derivatives are continuous and single-valued throughout V and s.
This may be written where n is a unit vector normal to the element of surface ds, and the symbol ∮ ∮S indicates that the integration is to be carried out over a closed surface. This theorem is sometimes called Green's theorem in the plane for the case of two-dimensional flow, and Green's theorem in space for the three-dimensional case described above. The divergence theorem is used extensively in manipulating the meteorological equations of motion.