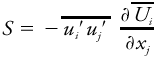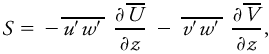Shear production: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == shear production == </div> <div class="definition"><div class="short_definition">The genera...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">The generation of [[turbulence kinetic energy]] caused by [[wind shear]].</div><br/> <div class="paragraph">This mechanical production term ''S'' of the turbulence kinetic energy budget equation is (written in [[Einstein's summation notation]]) <div class="display-formula"><blockquote>[[File:ams2001glos-Se20.gif|link=|center|ams2001glos-Se20]]</blockquote></div> and is almost always positive, that is, a source. In the fair-weather, turbulent [[atmospheric boundary layer]], the terms associated with horizontal wind usually dominate, allowing the shear production term to be approximated as <div class="display-formula"><blockquote>[[File:ams2001glos-Se21.gif|link=|center|ams2001glos-Se21]]</blockquote></div> where (<div class="inline-formula">[[File:ams2001glos-Sex03.gif|link=|ams2001glos-Sex03]]</div>,<div class="inline-formula">[[File:ams2001glos-Sex04.gif|link=|ams2001glos-Sex04]]</div>) are the [[Reynolds stresses]] (turbulent kinematic [[momentum fluxes]]) in the (''x'', ''y'') directions, (''U'', ''V'') are the respective wind components, the prime denotes [[deviation]] from the mean, and the overbar denotes an average. The ratio of the buoyant to the negative of the shear production terms is also known as the [[flux Richardson number]] and is a measure of [[dynamic stability]].</div><br/> </div> | <div class="definition"><div class="short_definition">The generation of [[turbulence kinetic energy]] caused by [[wind shear]].</div><br/> <div class="paragraph">This mechanical production term ''S'' of the turbulence kinetic energy budget equation is (written in [[Einstein's summation notation]]) <div class="display-formula"><blockquote>[[File:ams2001glos-Se20.gif|link=|center|ams2001glos-Se20]]</blockquote></div> and is almost always positive, that is, a source. In the fair-weather, turbulent [[atmospheric boundary layer|atmospheric boundary layer]], the terms associated with horizontal wind usually dominate, allowing the shear production term to be approximated as <div class="display-formula"><blockquote>[[File:ams2001glos-Se21.gif|link=|center|ams2001glos-Se21]]</blockquote></div> where (<div class="inline-formula">[[File:ams2001glos-Sex03.gif|link=|ams2001glos-Sex03]]</div>,<div class="inline-formula">[[File:ams2001glos-Sex04.gif|link=|ams2001glos-Sex04]]</div>) are the [[Reynolds stresses]] (turbulent kinematic [[momentum flux|momentum fluxes]]) in the (''x'', ''y'') directions, (''U'', ''V'') are the respective wind components, the prime denotes [[deviation]] from the mean, and the overbar denotes an average. The ratio of the buoyant to the negative of the shear production terms is also known as the [[flux Richardson number]] and is a measure of [[dynamic stability|dynamic stability]].</div><br/> </div> | ||
</div> | </div> | ||
Latest revision as of 16:52, 25 April 2012
shear production
The generation of turbulence kinetic energy caused by wind shear.
This mechanical production term S of the turbulence kinetic energy budget equation is (written in Einstein's summation notation) and is almost always positive, that is, a source. In the fair-weather, turbulent atmospheric boundary layer, the terms associated with horizontal wind usually dominate, allowing the shear production term to be approximated as where (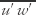
,
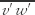) are the Reynolds stresses (turbulent kinematic momentum fluxes) in the (x, y) directions, (U, V) are the respective wind components, the prime denotes deviation from the mean, and the overbar denotes an average. The ratio of the buoyant to the negative of the shear production terms is also known as the flux Richardson number and is a measure of dynamic stability.
