Correlation

correlation

1. In general, a mutual relationship between variables or other entities.

   
   

   In statistical terminology, it is a form of statistical dependence.

   
   
2. When used without further qualification, the statistical term correlation usually refers to simple, linear correlation between two variables x, y and is measured by the product-moment coefficient of correlation ρ or its sample estimate r defined as follows, where the respective population mean values of x and y are denoted by ξ and ζ, the respective standard deviations by σ(x) and σ( y), and where E is the expected value:

   

   

   
   

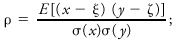
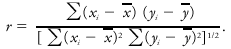   The product moment E[(x - ξ) (y - ζ)] is usually called the covariance of x and y. In connection with correlation, the word "simple" is used in contradistinction to other qualifiers such as "multiple" or "partial." The word "linear" refers to a linear relationship between the two variables, or more precisely, to a linear approximation of the regression function of either variate with respect to the other.
   See autocorrelation, multiple correlation, partial correlation.

   
   
3. 
   See correlation coefficient.

   
   

• INDEX
• A
• B
• C
• D
• E
• F
• G
• H
• I
• J
• K
• L
• M
• N
• O
• P
• Q
• R
• S
• T
• U
• V
• W
• X
• Y
• Z
• 0
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9