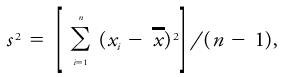Variance: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == variance == </div> <div class="definition"><div class="short_definition">A measure of varia...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">A measure of variability (or [[spread]]).</div><br/> <div class="paragraph">It is denoted by σ<sup>2</sup> and defined as the mean-square [[deviation]] from the mean, that is, the mean of the squares of the differences between individual values of ''x'' and the [[mean value]] μ: <div class="display-formula"><blockquote>[[File:ams2001glos-Ve3.gif|link=|center|ams2001glos-Ve3]]</blockquote></div> where ''E'' denotes [[expected value]]. The positive square root σ of the variance is called the [[standard deviation]]. An unbiased estimate ''s''<sup>2</sup> of the variance σ<sup>2</sup> is obtained from ''n'' independent observations ''x''<sub>1</sub>, ''x''<sub>2</sub>, · · ·, ''x''<sub>''n''</sub> and their [[sample]] average <div class="inline-formula">[[File:ams2001glos-Vex01.gif|link=|ams2001glos-Vex01]]</div> as follows: <div class="display-formula"><blockquote>[[File:ams2001glos-Ve4.gif|link=|center|ams2001glos-Ve4]]</blockquote></div> and the positive square root ''s'' of ''s''<sup>2</sup> is taken as an estimate of the standard deviation σ.</div><br/> </div> | <div class="definition"><div class="short_definition">A measure of variability (or [[spread]]).</div><br/> <div class="paragraph">It is denoted by σ<sup>2</sup> and defined as the mean-square [[deviation]] from the mean, that is, the mean of the squares of the differences between individual values of ''x'' and the [[mean value|mean value]] μ: <div class="display-formula"><blockquote>[[File:ams2001glos-Ve3.gif|link=|center|ams2001glos-Ve3]]</blockquote></div> where ''E'' denotes [[expected value]]. The positive square root σ of the variance is called the [[standard deviation|standard deviation]]. An unbiased estimate ''s''<sup>2</sup> of the variance σ<sup>2</sup> is obtained from ''n'' independent observations ''x''<sub>1</sub>, ''x''<sub>2</sub>, · · ·, ''x''<sub>''n''</sub> and their [[sample]] average <div class="inline-formula">[[File:ams2001glos-Vex01.gif|link=|ams2001glos-Vex01]]</div> as follows: <div class="display-formula"><blockquote>[[File:ams2001glos-Ve4.gif|link=|center|ams2001glos-Ve4]]</blockquote></div> and the positive square root ''s'' of ''s''<sup>2</sup> is taken as an estimate of the standard deviation σ.</div><br/> </div> | ||
</div> | </div> | ||
Latest revision as of 17:11, 25 April 2012
variance
A measure of variability (or spread).
It is denoted by σ2 and defined as the mean-square deviation from the mean, that is, the mean of the squares of the differences between individual values of x and the mean value μ: where E denotes expected value. The positive square root σ of the variance is called the standard deviation. An unbiased estimate s2 of the variance σ2 is obtained from n independent observations x1, x2, · · ·, xn and their sample average 
as follows: and the positive square root s of s2 is taken as an estimate of the standard deviation σ.
