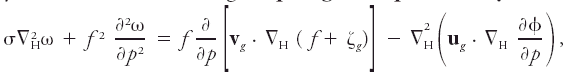Omega equation: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == omega equation == </div> <div class="definition"><div class="short_definition">A [[diagnost...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">A [[diagnostic equation]] by which the [[vertical velocity]] in [[pressure coordinates]] (ω = ''Dp''/''Dt'') may be calculated according to [[quasigeostrophic theory]]: <div class="display-formula"><blockquote>[[File:ams2001glos-Oe5.gif|link=|center|ams2001glos-Oe5]]</blockquote></div> for which ''f'' is the [[Coriolis parameter]], σ is the [[static stability]], '''v'''<sub>''g''</sub> is the [[geostrophic]] velocity [[vector]], ζ<sub>''g''</sub> is the geostrophic [[relative vorticity]], φ is the [[geopotential]], ∇<sub>H</sub><sup>2</sup> is the horizontal [[Laplacian operator]], and '''∇'''<sub>H</sub> is the horizontal [[del operator]].</div><br/> <div class="paragraph">The right-hand side of the omega equation can also be expressed in terms of the [[divergence]] of the '''Q''' [[vector]].</div><br/> </div><div class="reference">Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 166–175. </div><br/> | <div class="definition"><div class="short_definition">A [[diagnostic equation]] by which the [[vertical velocity]] in [[pressure coordinates]] (ω = ''Dp''/''Dt'') may be calculated according to [[quasigeostrophic theory]]: <div class="display-formula"><blockquote>[[File:ams2001glos-Oe5.gif|link=|center|ams2001glos-Oe5]]</blockquote></div> for which ''f'' is the [[Coriolis parameter]], σ is the [[static stability]], '''v'''<sub>''g''</sub> is the [[geostrophic]] velocity [[vector]], ζ<sub>''g''</sub> is the geostrophic [[relative vorticity]], φ is the [[geopotential]], ∇<sub>H</sub><sup>2</sup> is the horizontal [[Laplacian operator|Laplacian operator]], and '''∇'''<sub>H</sub> is the horizontal [[del operator]].</div><br/> <div class="paragraph">The right-hand side of the omega equation can also be expressed in terms of the [[divergence]] of the '''Q''' [[vector]].</div><br/> </div><div class="reference">Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 166–175. </div><br/> | ||
</div> | </div> | ||
Latest revision as of 16:32, 25 April 2012
omega equation
A diagnostic equation by which the vertical velocity in pressure coordinates (ω = Dp/Dt) may be calculated according to quasigeostrophic theory: for which f is the Coriolis parameter, σ is the static stability, vg is the geostrophic velocity vector, ζg is the geostrophic relative vorticity, φ is the geopotential, ∇H2 is the horizontal Laplacian operator, and ∇H is the horizontal del operator.
The right-hand side of the omega equation can also be expressed in terms of the divergence of the Q vector.
Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 166–175.