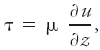Newtonian friction law: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == Newtonian friction law == </div> <div class="definition"><div class="short_definition">(<br...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">( | <div class="definition"><div class="short_definition">(''Also called'' Newton's formula for the [[stress]].) The statement that the tangential force (i.e., the force in the direction of the flow) per unit area acting at an arbitrary level within a fluid contained between two rigid horizontal plates, one of which is motionless and the other which is in [[steady motion]], is proportional to the [[shear]] of the fluid motion at that level.</div><br/> <div class="paragraph">Mathematically, the law is given by <div class="display-formula"><blockquote>[[File:ams2001glos-Ne5.gif|link=|center|ams2001glos-Ne5]]</blockquote></div> where τ is the tangential force per unit area, usually called the [[shearing stress]]; μ a constant of proportionality called the [[dynamic viscosity]]; and ∂''u''/∂''z'' the shear of the fluid flow normal to the resting plate. In deriving this expression Newton assumed that either the speed ''u'' of the moving plate or the distance between the plates was so small that, once a [[steady state]] was reached, the speed of the fluid increased linearly from zero at the resting plate to the speed ''u'' at the moving plate. In this case both the shear of the motion and the shearing stress are constant throughout the fluid.</div><br/> </div> | ||
</div> | </div> | ||
Latest revision as of 14:45, 20 February 2012
Newtonian friction law
(Also called Newton's formula for the stress.) The statement that the tangential force (i.e., the force in the direction of the flow) per unit area acting at an arbitrary level within a fluid contained between two rigid horizontal plates, one of which is motionless and the other which is in steady motion, is proportional to the shear of the fluid motion at that level.
Mathematically, the law is given by where τ is the tangential force per unit area, usually called the shearing stress; μ a constant of proportionality called the dynamic viscosity; and ∂u/∂z the shear of the fluid flow normal to the resting plate. In deriving this expression Newton assumed that either the speed u of the moving plate or the distance between the plates was so small that, once a steady state was reached, the speed of the fluid increased linearly from zero at the resting plate to the speed u at the moving plate. In this case both the shear of the motion and the shearing stress are constant throughout the fluid.