Froude number: Difference between revisions

Revision as of 07:31, 12 December 2014

Froude number

The nondimensional ratio of the inertial force to the force of gravity for a given fluid flow; the reciprocal of the Reech number.

It may be given as
where V is a characteristic velocity, L a characteristic length, and g the acceleration of gravity; or as the square root of this number.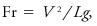
For continuously stratified, nonrotating, dry, inviscid 2D flow over an obstacle of height h, with incoming wind speed U, and upstream Brunt–Väisälä frequency N, the quantity U/(Nh) yields a measure of whether there will be an upstream-propagating region of decelerated flow and, hence, is also sometimes referred to as the Froude number. For U/(Nh) >> 1, the flow ascends over the obstacle with no upstream deceleration. For U/(Nh) << 1, a region of upstream flow deceleration forms that may propagate continuously upstream with time. Note that referring to the above relation as the Froude number is not consistent with the classical definition of Fr (see definition 1 above). For consistency with the original definition of Fr, some advocate referring to the relation Nh/U (the inverse of Fr as it is defined herein) as the nondimensional mountain height.

term edited 12 Dec 2014

INDEX
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
0
1
2
3
4
5
6
7
8
9

@@ Line 10: / Line 10: @@
 #<div class="definition"><div class="short_definition">The nondimensional ratio of the [[inertial force]] to the [[force of gravity]] for a  given fluid flow; the reciprocal of the [[Reech number]].</div><br/> <div class="paragraph">It may be given as  <div class="display-formula"><blockquote>[[File:ams2001glos-Fe21.gif|link=|center|ams2001glos-Fe21]]</blockquote></div> where ''V'' is a [[characteristic velocity]], ''L'' a [[characteristic length]], and ''g'' the [[acceleration of gravity]];   or as the square root of this number.</div><br/> </div>
-#<div class="definition"><div class="short_definition">For atmospheric flows over hills or other obstacles, a more useful form of the Froude number  is  <div class="display-formula"><blockquote>[[File:ams2001glos-Fe22.gif|link=|center|ams2001glos-Fe22]]</blockquote></div> where ''N''<sub>''BV''</sub> is the [[Brunt-väisälä frequency]] of the ambient [[upstream]] environment, ''V'' is the [[wind speed|wind  speed]] component across the mountain, and ''L''<sub>''w''</sub> is the width of the mountain. </div><br/> <div class="paragraph">Fr can be interpreted as the ratio of natural [[wavelength]] of the air to wavelength of the mountain.  Sometimes &#x003c0; will appear in the numerator, and other times the ratio will be squared. When Fr =  1, the natural wavelength of the air is in [[resonance]] with the size of the mountain and creates the  most intense [[mountain waves]], which can sometimes contain [[lenticular clouds]] and [[rotors]] of  reverse flow at the surface. For Fr &lt; 1, some of the low-altitude upstream air is blocked by the  hill, short-wavelength waves separate from the top of the hill, and the remaining air at lower  altitudes flows laterally around the hill. For Fr &gt; 1, very long wavelengths form [[downwind]] of the  hill, and can include a [[cavity]] of reverse flow just to the lee of the hill near the surface. Another  form of the Froude number, using (''z''<sub>''i''</sub> - ''z''<sub>''hill''</sub>) in place of ''L''<sub>''w''</sub>, is useful for diagnosing downslope  windstorms and [[hydraulic jump]], where ''z''<sub>''i''</sub> is the depth of the [[mixed layer]] above the base of the  mountain, and ''z''<sub>''hill''</sub> is the height of the mountain.</div><br/> </div>
+#<div class="definition"><div class="short_definition">For continuously stratified, nonrotating, dry, inviscid 2D flow over an obstacle of height ''h'', with incoming [[wind speed]] ''U'', and [[upstream]] [[Brunt–Väisälä frequency]] ''N'', the quantity ''U''/(''Nh'') yields a measure of whether there will be an upstream-propagating region of decelerated flow and, hence, is also sometimes referred to as the Froude number. For ''U''/(''Nh'') >> 1, the flow ascends over the obstacle with no upstream deceleration. For ''U''/(''Nh'') << 1, a region of upstream flow deceleration forms that may propagate continuously upstream with time. Note that referring to the above relation as the Froude number is not consistent with the classical definition of Fr (see definition 1 above). For consistency with the original definition of Fr, some advocate referring to the relation ''Nh''/''U'' (the inverse of Fr as it is defined herein) as the nondimensional mountain height.</div><br/>
-</div>
+</div><br/><br/>''term edited 12 Dec 2014''
 {{TermIndex}}