Gauss elimination: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == Gauss elimination == </div> <div class="definition"><div class="short_definition">A systema...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
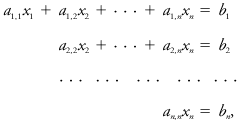
<div class="definition"><div class="short_definition">A systematic procedure for solving systems of [[linear]] algebraic equations of the form <div class="display-formula"><blockquote>[[File:ams2001glos-Ge11.gif|link=|center|ams2001glos-Ge11]]</blockquote></div> <div class="display-formula"><blockquote>[[File:ams2001glos-Ge12.gif|link=|center|ams2001glos-Ge12]]</blockquote></div> <div class="display-formula"><blockquote>[[File:ams2001glos-Ge13.gif|link=|center|ams2001glos-Ge13]]</blockquote></div> <div class="display-formula"><blockquote>[[File:ams2001glos-Ge14.gif|link=|center|ams2001glos-Ge14]]</blockquote></div> where the ''x''<sub>''j''</sub> represent unknown quantities and where the ''a''<sub>''i'',''j''</sub> and ''b''<sub>i</sub> are prescribed constants. Multiples of one equation are combined with another to eliminate variables successively until the system has the upper triangular form <div class="display-formula"><blockquote>[[File:ams2001glos-Ge15.gif|link=|center|ams2001glos-Ge15]]</blockquote></div> where the constants in all but the first equation have been altered by the elimination process. The last equation is solved for ''x''<sub>''n''</sub> and the resulting value substituted in the preceding equation which then can be solved for ''x''<sub>''n'' | <div class="definition"><div class="short_definition">A systematic procedure for solving systems of [[linear]] algebraic equations of the form <div class="display-formula"><blockquote>[[File:ams2001glos-Ge11.gif|link=|center|ams2001glos-Ge11]]</blockquote></div> <div class="display-formula"><blockquote>[[File:ams2001glos-Ge12.gif|link=|center|ams2001glos-Ge12]]</blockquote></div> <div class="display-formula"><blockquote>[[File:ams2001glos-Ge13.gif|link=|center|ams2001glos-Ge13]]</blockquote></div> <div class="display-formula"><blockquote>[[File:ams2001glos-Ge14.gif|link=|center|ams2001glos-Ge14]]</blockquote></div> where the ''x''<sub>''j''</sub> represent unknown quantities and where the ''a''<sub>''i'',''j''</sub> and ''b''<sub>i</sub> are prescribed constants. Multiples of one equation are combined with another to eliminate variables successively until the system has the upper triangular form <div class="display-formula"><blockquote>[[File:ams2001glos-Ge15.gif|link=|center|ams2001glos-Ge15]]</blockquote></div> where the constants in all but the first equation have been altered by the elimination process. The last equation is solved for ''x''<sub>''n''</sub> and the resulting value substituted in the preceding equation which then can be solved for ''x''<sub>''n''-1</sub>. The back-substitution process is continued until all the remaining unknowns are determined.</div><br/> </div> | ||
</div> | </div> | ||
Latest revision as of 14:18, 20 February 2012
Gauss elimination
A systematic procedure for solving systems of linear algebraic equations of the form where the xj represent unknown quantities and where the ai,j and bi are prescribed constants. Multiples of one equation are combined with another to eliminate variables successively until the system has the upper triangular form where the constants in all but the first equation have been altered by the elimination process. The last equation is solved for xn and the resulting value substituted in the preceding equation which then can be solved for xn-1. The back-substitution process is continued until all the remaining unknowns are determined.