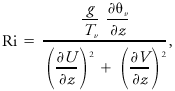Gradient richardson number: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == gradient Richardson number == </div> <div class="definition"><div class="short_definition">...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">A dimensionless ratio, Ri, related to the buoyant production or [[consumption]] of [[turbulence]] divided by the [[shear production]] of turbulence.</div><br/> <div class="paragraph">It is used to indicate [[dynamic stability]] and the formation of turbulence: <div class="display-formula"><blockquote>[[File:ams2001glos-Ge35.gif|link=|center|ams2001glos-Ge35]]</blockquote></div> where θ<sub>''v''</sub> is [[virtual potential temperature]], ''T''<sub>''v''</sub> is virtual absolute temperature, ''z'' is height, ''g'' is gravitational [[acceleration]], and (''U'', ''V'') are the [[wind]] components toward the east and north. The [[critical Richardson number]], Ri<sub>c</sub>, is about 0.25 (although reported values have ranged from roughly 0.2 to 1.0), and flow is dynamically unstable and turbulent when Ri < Ri<sub>c</sub>. Such turbulence happens either when the [[wind shear]] is great enough to overpower any stabilizing buoyant forces (numerator is positive), or when there is [[static instability]] (numerator is negative). <br/>''Compare'' [[bulk Richardson number]], [[flux Richardson number]], [[Froude number]].</div><br/> </div> | <div class="definition"><div class="short_definition">A dimensionless ratio, Ri, related to the buoyant production or [[consumption]] of [[turbulence]] divided by the [[shear production]] of turbulence.</div><br/> <div class="paragraph">It is used to indicate [[dynamic stability]] and the formation of turbulence: <div class="display-formula"><blockquote>[[File:ams2001glos-Ge35.gif|link=|center|ams2001glos-Ge35]]</blockquote></div> where θ<sub>''v''</sub> is [[virtual potential temperature]], ''T''<sub>''v''</sub> is virtual absolute temperature, ''z'' is height, ''g'' is gravitational [[acceleration]], and (''U'', ''V'') are the [[wind]] components toward the east and north. The [[critical Richardson number]], Ri<sub>c</sub>, is about 0.25 (although reported values have ranged from roughly 0.2 to 1.0), and flow is dynamically unstable and turbulent when Ri < Ri<sub>c</sub>. Such turbulence happens either when the [[wind shear]] is great enough to overpower any stabilizing buoyant forces (numerator is positive), or when there is [[static instability]] (numerator is negative). <br/>''Compare'' [[bulk Richardson number|bulk Richardson number]], [[flux Richardson number]], [[Froude number]].</div><br/> </div> | ||
</div> | </div> | ||
Revision as of 16:05, 25 April 2012
gradient Richardson number
A dimensionless ratio, Ri, related to the buoyant production or consumption of turbulence divided by the shear production of turbulence.
It is used to indicate dynamic stability and the formation of turbulence: where θv is virtual potential temperature, Tv is virtual absolute temperature, z is height, g is gravitational acceleration, and (U, V) are the wind components toward the east and north. The critical Richardson number, Ric, is about 0.25 (although reported values have ranged from roughly 0.2 to 1.0), and flow is dynamically unstable and turbulent when Ri < Ric. Such turbulence happens either when the wind shear is great enough to overpower any stabilizing buoyant forces (numerator is positive), or when there is static instability (numerator is negative).
Compare bulk Richardson number, flux Richardson number, Froude number.
Compare bulk Richardson number, flux Richardson number, Froude number.