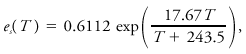Clausius-clapeyron equation: Difference between revisions
From Glossary of Meteorology
| Line 7: | Line 7: | ||
<div class="term"> | <div class="term"> | ||
== Clausius–Clapeyron equation == | == Clausius–Clapeyron equation == | ||
<div class="definition"><div class="short_definition">(''Also called'' Clapeyron equation, Clapeyron–Clausius equation.) The differential equation relating [[pressure]] of a substance to [[temperature]] in a system in which two phases of the substance are in [[equilibrium]].</div><br/> <div class="paragraph">Two general expressions are <div class="display-formula"><blockquote>[[File:ams2001glos-Ce17.gif|link=|center|ams2001glos-Ce17]]</blockquote></div> where ''p'' is the pressure, ''T'' the temperature, δ''s'' the difference in [[specific entropy]] between the phases, δ''v'' the difference in [[specific volume]] between the two phases, and ''L'' the [[latent heat]] of the [[phase change]]. The form most familiar in meteorology, related to the phase change between [[water vapor]] and liquid water, is obtained after some approximations as <div class="display-formula"><blockquote>[[File:ams2001glos-Ce18.gif|link=|center|ams2001glos-Ce18]]</blockquote></div> where ''e''<sub>''s''</sub> is the [[saturation vapor pressure]] of water, ''L''<sub>''v''</sub> the latent heat of [[vaporization]], and ''R''<sub>''v''</sub> the [[gas constant]] for water vapor. A similar relation for the saturation vapor pressure in contact with an [[ice]] surface is obtained by replacing the latent heat of vaporization by that of [[sublimation]]. These equations may be integrated to obtain explicit relationships between ''e''<sub>''s''</sub> and ''T'', given known values at some point. The most empirically accurate relationships differ slightly from results so obtained. An expression believed accurate to 0.3% for -35°C < ''T'' < 35°C is given by Bolton as <div class="display-formula"><blockquote>[[File:ams2001glos-Ce19.gif|link=|center|ams2001glos-Ce19]]</blockquote></div> where ''T'' is temperature in °C and [[vapor pressure]] is in kPa.</div><br/> </div><div class="reference">Iribarne, J. V., and W. L. Godson. 1981. ''Atmospheric Thermodynamics''. D. Reidel, p. 65. </div><br/> <div class="reference">Bolton, D. 1980. The computation of equivalent potential temperature. ''Mon. Wea. Rev.'', '''108'''. 1046–1053. </div><br/> | <div class="definition"><div class="short_definition">(''Also called'' Clapeyron equation, Clapeyron–Clausius equation.) The differential equation relating [[pressure]] of a substance to [[temperature]] in a system in which two phases of the substance are in [[equilibrium]].</div><br/> <div class="paragraph">Two general expressions are <div class="display-formula"><blockquote>[[File:ams2001glos-Ce17.gif|link=|center|ams2001glos-Ce17]]</blockquote></div> where ''p'' is the pressure, ''T'' the temperature, δ''s'' the difference in [[specific entropy]] between the phases, δ''v'' the difference in [[specific volume]] between the two phases, and ''L'' the [[latent heat]] of the [[phase change]]. The form most familiar in meteorology, related to the phase change between [[water vapor]] and liquid water, is obtained after some approximations as <div class="display-formula"><blockquote>[[File:ams2001glos-Ce18.gif|link=|center|ams2001glos-Ce18]]</blockquote></div> where ''e''<sub>''s''</sub> is the [[saturation vapor pressure]] of water, ''L''<sub>''v''</sub> the latent heat of [[vaporization]], and ''R''<sub>''v''</sub> the [[gas constant]] for water vapor. A similar relation for the saturation vapor pressure in contact with an [[ice]] surface is obtained by replacing the latent heat of vaporization by that of [[sublimation]]. These equations may be integrated to obtain explicit relationships between ''e''<sub>''s''</sub> and ''T'', given known values at some point. The most empirically accurate relationships differ slightly from results so obtained. An expression believed accurate to 0.3% for -35°C < ''T'' < 35°C is given by Bolton as <div class="display-formula"><blockquote>[[File:ams2001glos-Ce19.gif|link=|center|ams2001glos-Ce19]]</blockquote></div> where ''T'' is temperature in °C and [[vapor pressure]] is in kPa.</div><br/> </div><div class="reference">Iribarne, J. V., and W. L. Godson. 1981. ''Atmospheric Thermodynamics''. D. Reidel, p. 65. </div><br/> <div class="reference">Bolton, D. 1980. The computation of equivalent potential temperature. ''Mon. Wea. Rev.'', '''108'''. 1046–1053. </div><br/> | ||
</ | |||
<p>''Term edited 1 June 2022.''</p> | |||
{{TermIndex}} | {{TermIndex}} | ||
Latest revision as of 05:55, 1 June 2022
Clausius–Clapeyron equation
(Also called Clapeyron equation, Clapeyron–Clausius equation.) The differential equation relating pressure of a substance to temperature in a system in which two phases of the substance are in equilibrium.
Two general expressions are where p is the pressure, T the temperature, δs the difference in specific entropy between the phases, δv the difference in specific volume between the two phases, and L the latent heat of the phase change. The form most familiar in meteorology, related to the phase change between water vapor and liquid water, is obtained after some approximations as where es is the saturation vapor pressure of water, Lv the latent heat of vaporization, and Rv the gas constant for water vapor. A similar relation for the saturation vapor pressure in contact with an ice surface is obtained by replacing the latent heat of vaporization by that of sublimation. These equations may be integrated to obtain explicit relationships between es and T, given known values at some point. The most empirically accurate relationships differ slightly from results so obtained. An expression believed accurate to 0.3% for -35°C < T < 35°C is given by Bolton as where T is temperature in °C and vapor pressure is in kPa.
Iribarne, J. V., and W. L. Godson. 1981. Atmospheric Thermodynamics. D. Reidel, p. 65.
Bolton, D. 1980. The computation of equivalent potential temperature. Mon. Wea. Rev., 108. 1046–1053.
Term edited 1 June 2022.