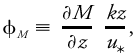Universal functions: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == universal functions == </div> <div class="definition"><div class="short_definition">Accordi...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">According to the [[Monin–Obukhov similarity theory]], the dimensionless [[shear]] <div class="display-formula"><blockquote>[[File:ams2001glos-Ue3.gif|link=|center|ams2001glos-Ue3]]</blockquote></div> [[temperature]] gradient <div class="display-formula"><blockquote>[[File:ams2001glos-Ue4.gif|link=|center|ams2001glos-Ue4]]</blockquote></div> and other gradients in the [[surface layer]] are proportional to dimensionless universal [[stability]] functions, where ''M'' is [[wind speed]], θ is [[potential temperature]], ''u''<sub>*</sub> is [[friction velocity]], and θ<sub>*</sub> is the surface kinematic [[heat flux]] divided by [[friction velocity]].</div><br/> <div class="paragraph">These functions have a value of nearly 1 for neutral [[stratification]], [[range]] over 0 < (''z''/''L'') < 1 for unstable stratification, and ''z''/''L'' > 1 for stable stratification, where ''z'' is height above the surface and ''L'' is the [[Obukhov length]]. For strong stability (''z''/''L'' >> 1) the universal functions are nearly constant. Presently the most-used universal functions are based on an experiment conducted in Kansas in 1968, with some corrections made in the succeeding 30 years. The [[accuracy]] is about 10% for unstable and 20% for stable stratification. The following empirical forms of the universal functions, based on a von [[K& | <div class="definition"><div class="short_definition">According to the [[Monin–Obukhov similarity theory]], the dimensionless [[shear]] <div class="display-formula"><blockquote>[[File:ams2001glos-Ue3.gif|link=|center|ams2001glos-Ue3]]</blockquote></div> [[temperature]] gradient <div class="display-formula"><blockquote>[[File:ams2001glos-Ue4.gif|link=|center|ams2001glos-Ue4]]</blockquote></div> and other gradients in the [[surface layer]] are proportional to dimensionless universal [[stability]] functions, where ''M'' is [[wind speed]], θ is [[potential temperature]], ''u''<sub>*</sub> is [[friction velocity]], and θ<sub>*</sub> is the surface kinematic [[heat flux]] divided by [[friction velocity]].</div><br/> <div class="paragraph">These functions have a value of nearly 1 for neutral [[stratification]], [[range]] over 0 < (''z''/''L'') < 1 for unstable stratification, and ''z''/''L'' > 1 for stable stratification, where ''z'' is height above the surface and ''L'' is the [[Obukhov length]]. For strong stability (''z''/''L'' >> 1) the universal functions are nearly constant. Presently the most-used universal functions are based on an experiment conducted in Kansas in 1968, with some corrections made in the succeeding 30 years. The [[accuracy]] is about 10% for unstable and 20% for stable stratification. The following empirical forms of the universal functions, based on a von [[Kármán constant]] of k = 0.4, are currently used. For unstable stratification: <div class="display-formula"><blockquote>[[File:ams2001glos-Ue5.gif|link=|center|ams2001glos-Ue5]]</blockquote></div>For neutral stratification: <div class="display-formula"><blockquote>[[File:ams2001glos-Ue7.gif|link=|center|ams2001glos-Ue7]]</blockquote></div>For stable stratification: <div class="display-formula"><blockquote>[[File:ams2001glos-Ue9.gif|link=|center|ams2001glos-Ue9]]</blockquote></div>These universal functions are <br/>''also called'' [[flux-profile relationships]].</div><br/> </div> | ||
</div> | </div> | ||
Latest revision as of 15:23, 20 February 2012
universal functions
According to the Monin–Obukhov similarity theory, the dimensionless shear temperature gradient and other gradients in the surface layer are proportional to dimensionless universal stability functions, where M is wind speed, θ is potential temperature, u* is friction velocity, and θ* is the surface kinematic heat flux divided by friction velocity.
These functions have a value of nearly 1 for neutral stratification, range over 0 < (z/L) < 1 for unstable stratification, and z/L > 1 for stable stratification, where z is height above the surface and L is the Obukhov length. For strong stability (z/L >> 1) the universal functions are nearly constant. Presently the most-used universal functions are based on an experiment conducted in Kansas in 1968, with some corrections made in the succeeding 30 years. The accuracy is about 10% for unstable and 20% for stable stratification. The following empirical forms of the universal functions, based on a von Kármán constant of k = 0.4, are currently used. For unstable stratification: For neutral stratification: For stable stratification: These universal functions are
also called flux-profile relationships.
also called flux-profile relationships.