Power spectrum

power spectrum

1. The square of the amplitude of the (complex) Fourier coefficient of a given periodic function.

   
   

   Thus if f(t) is periodic with period T, its Fourier coefficients are

   

   where ω = 2π/T, and the power spectrum of f(t) is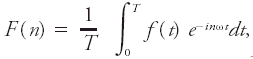

   

   . Here n takes integral values and the spectrum is discrete. The total energy of the periodic function is infinite, but the power, or energy per unit period, is finite. In the case of the aperiodic function containing finite total energy, the energy density spectrum is the corresponding spectral function. This is a continuous function of frequency and therefore has dimensions of energy/frequency (energy density). In the case of a random function containing infinite total energy but not periodic, the power density spectrum is the corresponding spectral function. The mathematical conditions governing analogous theorems in these three classes of functions are different. However, when actual computations of observational data are involved, a finite number of discrete values are used, and the effect is the same as if the function were assumed to be periodic outside the interval of computation. Thus, it is the power spectrum that is exhibited. But all types of spectra referred to may be considered as measures of the contribution of given frequencies in the Fourier representation of the original function. The terms "power" and "energy" are usually retained to indicate relative dimensions regardless of the actual dimensions of the functions analyzed, which may be functions of space as well as time. Computation of the power spectrum in practice may be facilitated by use of the theorem that it is the Fourier coefficient of the autocorrelation function.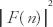

   
   
2. 
   Same as power density spectrum.

   
   

• INDEX
• A
• B
• C
• D
• E
• F
• G
• H
• I
• J
• K
• L
• M
• N
• O
• P
• Q
• R
• S
• T
• U
• V
• W
• X
• Y
• Z
• 0
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9