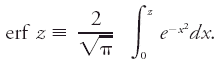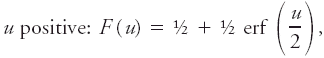Probability integral
From Glossary of Meteorology
probability integral
The classical form (still widely used in engineering work) of the definite integral of the special normal distribution for which the mean μ = 0 and standard deviation σ = 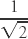 .
.
Geometrically, the probability integral equals the area under this density curve between -z and z, where z is an arbitrary positive number. Often denoted by the symbol erf z (read "error function of z") the probability integral is defined thus: Modern statistical usage favors the unit normal variate u, which is such that μ = 0 and σ = 1. The relation between the probability integral erf z and the distribution function F(u) of the unit normal variate u is as follows:
See unit normal distribution.
See unit normal distribution.