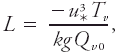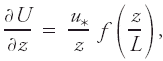Monin-obukhov similarity theory

Monin–Obukhov similarity theory

A relationship describing the vertical behavior of nondimensionalized mean flow and turbulence properties within the atmospheric surface layer (the lowest 10% or so of the atmospheric boundary layer) as a function of the Monin–Obukhov key parameters.

These key parameters are the height z above the surface, the buoyancy parameter ratio g/T_v of inertia and buoyancy forces, the kinematic surface stress τ₀/ρ, and the surface virtual temperature flux

where g is gravitational acceleration, T_v is virtual temperature, τ₀ is turbulent stress at the surface, ρ is air density, Q_v0 is a kinematic virtual heat flux at the surface, H_v0 is a dynamic virtual heat flux at the surface, C_p is the specific heat of air at constant pressure, and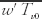

is the covariance of vertical velocity w with virtual temperature near the surface. The key parameters can be used to define a set of four dimensional scales for the surface layer: 1) the friction velocity or shearing velocity, a velocity scale,

2) a surface-layer temperature scale,

3) a length scale called the Obukhov length,

where k is the von Kármán constant; and 4) the height above ground scale, z. These key scales can then be used in dimensional analysis to express all surface-layer flow properties as dimensionless universal functions of z/L. For example, the mean wind shear in any quasi-stationary, locally homogeneous surface layer can be written as

where f is a universal function of the dimensionless height z/L. The forms of the universal functions are not given by the Monin–Obukhov theory, but must be determined theoretically or empirically. Monin–Obukhov similarity theory is the basic similarity hypothesis for the horizontally homogeneous surface layer. With these equations and the hypothesis that the fluxes in the surface layer are uniform with height, the momentum flux, sensible heat flux, and fluxes of water vapor and other gases can be determined.
Compare aerodynamic roughness length, Richardson number.

• INDEX
• A
• B
• C
• D
• E
• F
• G
• H
• I
• J
• K
• L
• M
• N
• O
• P
• Q
• R
• S
• T
• U
• V
• W
• X
• Y
• Z
• 0
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9

1. That property of an object that enables it to float on the surface of a liquid, or ascend through and remain freely suspended in a compressible fluid such as the atmosphere.