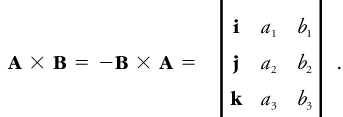Vector product

From Glossary of Meteorology
(Redirected from Cross product)



vector product

(Also called cross product, outer product.) A vector with magnitude equal to the product of the magnitudes of any two given vectors and the sine of the angle between their positive directions.

For two vectors A and B, the vector product is often written A × B (read "A cross B"), and defines a vector perpendicular to both A and B and so directed that a right-hand rotation about A × B through an angle of not more than 180° carries A into B. The magnitude of A × B is equal to twice the area of the triangle of which A and B are coterminous sides. If the vector product is zero, either one of the vectors is zero or the two are parallel. When A and B are written in terms of their components along the x, y, and z axes of the rectangular Cartesian coordinates, that is,
ams2001glos-Ve6
ams2001glos-Ve7
then the vector product is the determinant
ams2001glos-Ve8

See scalar product.


Retrieved from "https://glossarystaging.ametsoc.net/w/index.php?title=Vector_product&oldid=4116"
Powered by MediaWiki
Powered by WikiTeq
Powered by Semantic MediaWiki
Copyright 2024 American Meteorological Society (AMS). For permission to reuse any portion of this work, please contact permissions@ametsoc.org. Any use of material in this work that is determined to be “fair use” under Section 107 of the U.S. Copyright Act (17 U.S. Code § 107) or that satisfies the conditions specified in Section 108 of the U.S.Copyright Act (17 USC § 108) does not require AMS’s permission. Republication, systematic reproduction, posting in electronic form, such as on a website or in a searchable database, or other uses of this material, except as exempted by the above statement, require written permission or a license from AMS. Additional details are provided in the AMS Copyright Policy statement.