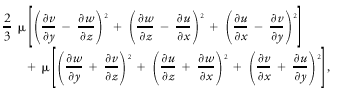Dissipation: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == dissipation == </div> <div class="definition"><div class="short_definition">(<br/>''Also ca...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">( | <div class="definition"><div class="short_definition">(''Also called'' [[viscous dissipation]].) In [[thermodynamics]], the conversion of [[kinetic energy]] into [[internal energy]] by [[work]] done against the [[viscous stresses]].</div><br/> <div class="paragraph">Sometimes the rate of conversion per unit volume is meant. If the [[Navier–Stokes equations]] of viscous flow are employed, Rayleigh's mathematical expression for the rate of viscous (or frictional) dissipation per unit volume is <div class="display-formula"><blockquote>[[File:ams2001glos-De26.gif|link=|center|ams2001glos-De26]]</blockquote></div> where μ is the [[dynamic viscosity]]. The Navier–Stokes assumptions thus satisfy the primary requirement of the [[second law of thermodynamics]] that the rate of dissipation be positive and the process irreversible. In a turbulent fluid, which the [[atmosphere]] usually is, dissipation is the end result of the turbulent scale process, by which kinetic energy is transferred from its originating, or outer, scale to the dissipation scales by nonlinear dynamical interactions. Most dissipation occurs at scales near the [[Kolmogorov microscale]] λ<sub>''d''</sub>, given by <div class="display-formula"><blockquote>[[File:ams2001glos-De27.gif|link=|center|ams2001glos-De27]]</blockquote></div> where ν is the [[kinematic viscosity]] and ε is the rate of [[energy]] dissipation per unit mass. <br/>''See also'' [[stress tensor]], [[energy equation]].</div><br/> </div><div class="reference">Brunt, D. 1941. Physical and Dynamical Meteorology. 285–286. </div><br/> | ||
</div> | </div> | ||
Revision as of 14:04, 20 February 2012
dissipation
(Also called viscous dissipation.) In thermodynamics, the conversion of kinetic energy into internal energy by work done against the viscous stresses.
Sometimes the rate of conversion per unit volume is meant. If the Navier–Stokes equations of viscous flow are employed, Rayleigh's mathematical expression for the rate of viscous (or frictional) dissipation per unit volume is where μ is the dynamic viscosity. The Navier–Stokes assumptions thus satisfy the primary requirement of the second law of thermodynamics that the rate of dissipation be positive and the process irreversible. In a turbulent fluid, which the atmosphere usually is, dissipation is the end result of the turbulent scale process, by which kinetic energy is transferred from its originating, or outer, scale to the dissipation scales by nonlinear dynamical interactions. Most dissipation occurs at scales near the Kolmogorov microscale λd, given by where ν is the kinematic viscosity and ε is the rate of energy dissipation per unit mass.
See also stress tensor, energy equation.
See also stress tensor, energy equation.
Brunt, D. 1941. Physical and Dynamical Meteorology. 285–286.