Gradient transport theory: Difference between revisions

Latest revision as of 16:05, 25 April 2012

gradient transport theory

A first-order turbulence closure approximation that assumes that turbulent fluxes of any variable flow down the local gradient of that mean variable; analogous to molecular transport.

This local turbulence closure approach assumes that turbulence consists of only small eddies, causing diffusion-like transport. An example is

where the vertical kinematic flux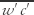

of a pollutant is modeled as being equal to an eddy thermal diffusivity K times the vertical gradient of mean concentration

. This theory is
also called K- theory or eddy-viscosity theory.
Compare higher-order closure, nonlocal closure, transilient turbulence theory.

INDEX
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
0
1
2
3
4
5
6
7
8
9

@@ Line 9: / Line 9: @@
    </div>
-<div class="definition"><div class="short_definition">A first-order [[turbulence closure]] approximation that assumes that turbulent  fluxes of any variable flow down the local [[gradient]] of that mean variable; analogous to  molecular [[transport]].</div><br/> <div class="paragraph">This local turbulence closure approach assumes that [[turbulence]] consists of only small [[eddies]],  causing diffusion-like [[transport]]. An example is  <div class="display-formula"><blockquote>[[File:ams2001glos-Ge36.gif|link=|center|ams2001glos-Ge36]]</blockquote></div> where the vertical [[kinematic flux]] <div class="inline-formula">[[File:ams2001glos-Gex03.gif|link=|ams2001glos-Gex03]]</div> of a [[pollutant]] is modeled as being equal to an eddy thermal  diffusivity ''K'' times the vertical gradient of mean concentration <div class="inline-formula">[[File:ams2001glos-Gex04.gif|link=|ams2001glos-Gex04]]</div>. This theory is <br/>''also called'' [[K-  theory]] or eddy-viscosity theory. <br/>''Compare'' [[higher-order closure]], [[nonlocal closure]], [[transilient  turbulence theory]].</div><br/> </div>
+<div class="definition"><div class="short_definition">A first-order [[turbulence closure]] approximation that assumes that turbulent  fluxes of any variable flow down the local [[gradient]] of that mean variable; analogous to  molecular [[transport]].</div><br/> <div class="paragraph">This local turbulence closure approach assumes that [[turbulence]] consists of only small [[eddies]],  causing diffusion-like [[transport]]. An example is  <div class="display-formula"><blockquote>[[File:ams2001glos-Ge36.gif|link=|center|ams2001glos-Ge36]]</blockquote></div> where the vertical [[kinematic flux]] <div class="inline-formula">[[File:ams2001glos-Gex03.gif|link=|ams2001glos-Gex03]]</div> of a [[pollutant]] is modeled as being equal to an eddy thermal  diffusivity ''K'' times the vertical gradient of mean concentration <div class="inline-formula">[[File:ams2001glos-Gex04.gif|link=|ams2001glos-Gex04]]</div>. This theory is <br/>''also called'' [[K-theory|K-  theory]] or eddy-viscosity theory. <br/>''Compare'' [[higher-order closure]], [[nonlocal closure]], [[transilient turbulence theory|transilient  turbulence theory]].</div><br/> </div>
 </div>