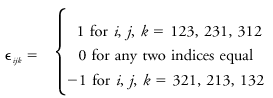Alternating unit tensor: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == alternating unit tensor == </div> <div class="definition"><div class="short_definition">A m...") |
m (Rewrite with Template:Term and clean up) |
||
| Line 1: | Line 1: | ||
{{Term | |||
|Display title=alternating unit tensor | |||
{{ | |Definitions={{Definition | ||
|Num=1 | |||
|Meaning= | |||
A mathematical function with symbol ε<sub>''ijk''</sub> defined to switch between the discrete values of +1, 0, and -1, depending on the values of the three indices ''i'', ''j'', and ''k'':<br/> <blockquote>[[File:ams2001glos-Ae16.gif|link=|center|ams2001glos-Ae16]]</blockquote> It is one of the tools used in [[Einstein's summation notation]] to handle operations equivalent to cross products in [[vector]] notation. For example: '''A''' × '''B''' = ε<sub>''ijk''</sub>''A''<sub>''i''</sub>''B''<sub>''j''</sub>δ<sub>''k''</sub>, where ''A''<sub>''i''</sub> and ''B''<sub>''j''</sub> represent vectors in [[summation notation]], and δ<sub>''k''</sub> is the unit vector. Subscripts or indices ''i'', ''j'', and ''k'' must each take on the values of 1, 2, and 3, representing the Cartesian directions of ''x'', ''y'', and ''z''. The alternating unit tensor is useful to describe the Coriolis term in the [[equations of motion]]: ∂''U''<sub>''i''</sub>/ ∂''t'' = . . . + ''f''ε<sub>''ij''3</sub>''U''<sub>''j''</sub> + . . ., where ''f'' is the [[Coriolis parameter]], ''U''<sub>''i''</sub> and ''U''<sub>''j''</sub> are [[wind]] components, and ''t'' is time. Summation notation is commonly used in [[atmospheric turbulence]] studies.<br/> Stull, R. B. 1988. An Introduction to Boundary Layer Meteorology. 666 pp. | |||
}} | |||
}} | |||
Revision as of 16:25, 7 November 2023
A mathematical function with symbol εijk defined to switch between the discrete values of +1, 0, and -1, depending on the values of the three indices i, j, and k:
Stull, R. B. 1988. An Introduction to Boundary Layer Meteorology. 666 pp.
It is one of the tools used in Einstein's summation notation to handle operations equivalent to cross products in vector notation. For example: A × B = εijkAiBjδk, where Ai and Bj represent vectors in summation notation, and δk is the unit vector. Subscripts or indices i, j, and k must each take on the values of 1, 2, and 3, representing the Cartesian directions of x, y, and z. The alternating unit tensor is useful to describe the Coriolis term in the equations of motion: ∂Ui/ ∂t = . . . + fεij3Uj + . . ., where f is the Coriolis parameter, Ui and Uj are wind components, and t is time. Summation notation is commonly used in atmospheric turbulence studies.
Stull, R. B. 1988. An Introduction to Boundary Layer Meteorology. 666 pp.