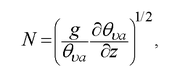Brunt-väisälä frequency: Difference between revisions
imported>Liss45 |
m (Rewrite with Template:Term and clean up) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
== Brunt–Väisälä frequency == | == Brunt–Väisälä frequency == | ||
The [[frequency]] ''N'' at which a displaced [[air parcel]] will oscillate when displaced vertically within a [[static stability|statically stable]] environment.<br/> It is given as <blockquote>[[File:Brunt_V_final.png|170px|center]]</blockquote> where ''g'' = 9.8 m s<sup>-1</sup> is gravitational [[acceleration]], ''θ''<sub>''υa''</sub> is the ambient virtual potential temperature, and ∂''θ''<sub>''υa''</sub>/∂''z'' is the vertical [[gradient]] of the ambient [[virtual potential temperature]]. Units are radians per second, although this is usually abbreviated as s<sup>-1</sup>. This frequency is not defined in statically [[unstable air]] and is zero in statically neutral air. The frequency of internal [[gravity waves]] in the [[atmosphere]] cannot exceed the local Brunt–Väisälä frequency. This frequency is also sometimes used as a measure of the [[stability]] within a statically stable environment.<br/> | |||
<br/>''See also'' [[buoyancy frequency]].<br/>Reference:Stull, R. B. 1995. Meteorology Today for Scientists and Engineers. 385 pp. <br/> | |||
''term edited 15 Dec 2014'' | ''term edited 15 Dec 2014'' | ||
Latest revision as of 22:20, 13 January 2024
Brunt–Väisälä frequency
The frequency N at which a displaced air parcel will oscillate when displaced vertically within a statically stable environment.
It is given as
where g = 9.8 m s-1 is gravitational acceleration, θυa is the ambient virtual potential temperature, and ∂θυa/∂z is the vertical gradient of the ambient virtual potential temperature. Units are radians per second, although this is usually abbreviated as s-1. This frequency is not defined in statically unstable air and is zero in statically neutral air. The frequency of internal gravity waves in the atmosphere cannot exceed the local Brunt–Väisälä frequency. This frequency is also sometimes used as a measure of the stability within a statically stable environment.
See also buoyancy frequency.
Reference:Stull, R. B. 1995. Meteorology Today for Scientists and Engineers. 385 pp.
term edited 15 Dec 2014