Perturbation technique

perturbation technique

A mathematical technique to eliminate linear terms in an equation in order to retain the nonlinear (turbulence) terms.

Variables such as potential temperature (θ) or velocity (U) can be partitioned into mean (slowly varying) and perturbation (rapidly varying) components. Mean components or averages are often represented with an overbar, while perturbation quantities are indicated with a prime:

When substituted in the equations of motion or other budget equations, the resulting equations have terms that explicitly describe the mean and turbulence components, and the interaction between these components. Next, the whole perturbation equation can be averaged, which eliminates the linear terms (terms having only one perturbation variable, such as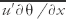

). The remaining nonlinear terms (terms that have products of two or more perturbation quantities, such as

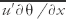) represent turbulent fluxes, variances, or correlations.
Compare ensemble average, area average, Reynolds averaging.

Starr, V. P. 1966. Physics of Negative Viscosity Phenomena. McGraw-Hill Pub. Co., . 256 pp.

Stull, R. B. 1988. An Introduction to Boundary Layer Meteorology. 666 pp.

• INDEX
• A
• B
• C
• D
• E
• F
• G
• H
• I
• J
• K
• L
• M
• N
• O
• P
• Q
• R
• S
• T
• U
• V
• W
• X
• Y
• Z
• 0
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9