Rossby wave: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot No edit summary |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">(''Also called'' planetary wave.) A [[wave]] on a uniform [[current]] in a two-dimensional nondivergent fluid system, rotating with varying angular speed about the local vertical ([[beta plane]]).</div><br/> <div class="paragraph">This is a special case of a [[barotropic disturbance]], conserving [[absolute vorticity]]. Applied to atmospheric flow, it takes into account the [[variability]] of the [[Coriolis parameter]] while assuming the motion to be two-dimensional. The [[wave speed]] c is given by <div class="display-formula"><blockquote>[[File:ams2001glos-Re49.gif|link=|center|ams2001glos-Re49]]</blockquote></div> where <div class="inline-formula">[[File:ams2001glos-Rex15.gif|link=|ams2001glos-Rex15]]</div> is the mean westerly flow, β is the [[Rossby parameter]], and ''K''<sup>2</sup> = ''k''<sup>2</sup> + ''l''<sup>2</sup>, the total [[wavenumber]] squared. (This formula is known as the Rossby formula, long-wave formula, or planetary-wave formula.) A stationary Rossby wave is thus of the order of the distance between the large-scale semipermanent [[troughs]] and [[ridges]] in the middle [[troposphere]]. The Rossby wave moves westward relative to the current, in effect slowing the eastward movement of long-wave components relative to the short-wave components in a [[barotropic]] flow. This effect is important in a numerical forecast with a [[barotropic model]], but attempts to apply the formula to actual [[contour]] patterns considered as waves have less dynamic justification and correspondingly less success. <br/>''See'' [[long wave]].</div><br/> </div><div class="reference">Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 216–222. </div><br/> | <div class="definition"><div class="short_definition">(''Also called'' planetary wave.) A [[wave]] on a uniform [[current]] in a two-dimensional nondivergent fluid system, rotating with varying angular speed about the local vertical ([[beta-plane|beta plane]]).</div><br/> <div class="paragraph">This is a special case of a [[barotropic disturbance]], conserving [[absolute vorticity]]. Applied to atmospheric flow, it takes into account the [[variability]] of the [[Coriolis parameter]] while assuming the motion to be two-dimensional. The [[wave speed]] c is given by <div class="display-formula"><blockquote>[[File:ams2001glos-Re49.gif|link=|center|ams2001glos-Re49]]</blockquote></div> where <div class="inline-formula">[[File:ams2001glos-Rex15.gif|link=|ams2001glos-Rex15]]</div> is the mean westerly flow, β is the [[Rossby parameter]], and ''K''<sup>2</sup> = ''k''<sup>2</sup> + ''l''<sup>2</sup>, the total [[wavenumber]] squared. (This formula is known as the Rossby formula, long-wave formula, or planetary-wave formula.) A stationary Rossby wave is thus of the order of the distance between the large-scale semipermanent [[troughs]] and [[ridges]] in the middle [[troposphere]]. The Rossby wave moves westward relative to the current, in effect slowing the eastward movement of long-wave components relative to the short-wave components in a [[barotropic]] flow. This effect is important in a numerical forecast with a [[barotropic model]], but attempts to apply the formula to actual [[contour]] patterns considered as waves have less dynamic justification and correspondingly less success. <br/>''See'' [[long wave]].</div><br/> </div><div class="reference">Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 216–222. </div><br/> | ||
</div> | </div> | ||
Latest revision as of 16:48, 25 April 2012
Rossby wave
(Also called planetary wave.) A wave on a uniform current in a two-dimensional nondivergent fluid system, rotating with varying angular speed about the local vertical (beta plane).
This is a special case of a barotropic disturbance, conserving absolute vorticity. Applied to atmospheric flow, it takes into account the variability of the Coriolis parameter while assuming the motion to be two-dimensional. The wave speed c is given by where 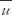 is the mean westerly flow, β is the Rossby parameter, and K2 = k2 + l2, the total wavenumber squared. (This formula is known as the Rossby formula, long-wave formula, or planetary-wave formula.) A stationary Rossby wave is thus of the order of the distance between the large-scale semipermanent troughs and ridges in the middle troposphere. The Rossby wave moves westward relative to the current, in effect slowing the eastward movement of long-wave components relative to the short-wave components in a barotropic flow. This effect is important in a numerical forecast with a barotropic model, but attempts to apply the formula to actual contour patterns considered as waves have less dynamic justification and correspondingly less success.
is the mean westerly flow, β is the Rossby parameter, and K2 = k2 + l2, the total wavenumber squared. (This formula is known as the Rossby formula, long-wave formula, or planetary-wave formula.) A stationary Rossby wave is thus of the order of the distance between the large-scale semipermanent troughs and ridges in the middle troposphere. The Rossby wave moves westward relative to the current, in effect slowing the eastward movement of long-wave components relative to the short-wave components in a barotropic flow. This effect is important in a numerical forecast with a barotropic model, but attempts to apply the formula to actual contour patterns considered as waves have less dynamic justification and correspondingly less success.
See long wave.
See long wave.
Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 216–222.
