Inertial instability: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == inertial instability == </div> #<div class="definition"><div class="short_definition">(<br/...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
#<div class="definition"><div class="short_definition">( | #<div class="definition"><div class="short_definition">(''Also called'' dynamic instability.) Generally, [[instability]] in which the only form of [[energy]] transferred between the [[steady state]] and the [[disturbance]] is [[kinetic energy]].</div><br/> <div class="paragraph"><br/>''See'' [[Helmholtz instability]], [[barotropic instability]].</div><br/> </div> | ||
#<div class="definition"><div class="short_definition">The [[hydrodynamic instability]] arising in a rotating fluid mass when the [[velocity distribution]] is such that the [[kinetic energy]] of a [[disturbance]] grows at the expense of kinetic energy of the rotation.</div><br/> <div class="paragraph">For a small plane-symmetric displacement ([[wavenumber]] zero) using the [[parcel method]], this criterion for [[instability]] is that the [[centrifugal force]] on the displaced parcels is larger than the centrifugal force acting on the [[environment]]. On the assumption that [[absolute angular momentum]] is conserved, this states that the fluid is unstable if absolute angular momentum decreases outward from the axis; <div class="display-formula"><blockquote>[[File:ams2001glos-Ie8.gif|link=|center|ams2001glos-Ie8]]</blockquote></div> where ω<sub>''a''</sub> is the [[absolute]] angular speed and ''R'' the distance from the axis. If this criterion is applied to rotation of the [[westerlies]] about the earth's axis, the angular speed of the earth is so large that the inequality fails and the [[disturbance]] is stable. If applied to a system rotating about a local vertical, the criterion might be satisfied in low latitudes where the component of the earth's rotation about the local vertical is small. Inertial instability has been suggested in connection with the genesis of hurricanes. <br/>''See'' [[rotational instability]].</div><br/> </div><div class="reference">Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 207–208. </div><br/> <div class="reference">Eliassen, A., and E. Kleinschmidt 1957. Dynamic Meteorology. Handbuch der Geophysik. Vol. XLVIII, . 64– 72. </div><br/> | #<div class="definition"><div class="short_definition">The [[hydrodynamic instability]] arising in a rotating fluid mass when the [[velocity distribution]] is such that the [[kinetic energy]] of a [[disturbance]] grows at the expense of kinetic energy of the rotation.</div><br/> <div class="paragraph">For a small plane-symmetric displacement ([[wavenumber]] zero) using the [[parcel method]], this criterion for [[instability]] is that the [[centrifugal force]] on the displaced parcels is larger than the centrifugal force acting on the [[environment]]. On the assumption that [[absolute angular momentum]] is conserved, this states that the fluid is unstable if absolute angular momentum decreases outward from the axis; <div class="display-formula"><blockquote>[[File:ams2001glos-Ie8.gif|link=|center|ams2001glos-Ie8]]</blockquote></div> where ω<sub>''a''</sub> is the [[absolute]] angular speed and ''R'' the distance from the axis. If this criterion is applied to rotation of the [[westerlies]] about the earth's axis, the angular speed of the earth is so large that the inequality fails and the [[disturbance]] is stable. If applied to a system rotating about a local vertical, the criterion might be satisfied in low latitudes where the component of the earth's rotation about the local vertical is small. Inertial instability has been suggested in connection with the genesis of hurricanes. <br/>''See'' [[rotational instability]].</div><br/> </div><div class="reference">Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 207–208. </div><br/> <div class="reference">Eliassen, A., and E. Kleinschmidt 1957. Dynamic Meteorology. Handbuch der Geophysik. Vol. XLVIII, . 64– 72. </div><br/> | ||
</div> | </div> | ||
Latest revision as of 14:28, 20 February 2012
inertial instability[edit | edit source]
- (Also called dynamic instability.) Generally, instability in which the only form of energy transferred between the steady state and the disturbance is kinetic energy.
- The hydrodynamic instability arising in a rotating fluid mass when the velocity distribution is such that the kinetic energy of a disturbance grows at the expense of kinetic energy of the rotation.
For a small plane-symmetric displacement (wavenumber zero) using the parcel method, this criterion for instability is that the centrifugal force on the displaced parcels is larger than the centrifugal force acting on the environment. On the assumption that absolute angular momentum is conserved, this states that the fluid is unstable if absolute angular momentum decreases outward from the axis;where ωa is the absolute angular speed and R the distance from the axis. If this criterion is applied to rotation of the westerlies about the earth's axis, the angular speed of the earth is so large that the inequality fails and the disturbance is stable. If applied to a system rotating about a local vertical, the criterion might be satisfied in low latitudes where the component of the earth's rotation about the local vertical is small. Inertial instability has been suggested in connection with the genesis of hurricanes.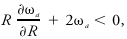
See rotational instability.
Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 207–208.
Eliassen, A., and E. Kleinschmidt 1957. Dynamic Meteorology. Handbuch der Geophysik. Vol. XLVIII, . 64– 72.
