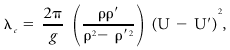Helmholtz instability

(Also called shearing instability.) The hydrodynamic instability arising from a shear, or discontinuity, in current speed at the interface between two fluids in two-dimensional motion.

The perturbation gains kinetic energy at the expense of that of the basic currents. According to the theory of small perturbations, waves of all wavelengths on such an interface are unstable, their rate of growth being e^μt with μ given by

where λ is the wavelength and U and U′ the current speeds of the two fluids. Such waves are called Helmholtz waves or shear waves, and move with a phase speed c equal to the mean of the current speeds,

With an assumed density difference in the fluids, gravity waves may also be generated. The combination of these effects yields a critical wavelength λ_c,

where ρ and ρ′ are the densities of the lower and upper fluids, respectively. Waves shorter than the critical are unstable, longer waves, stable. This analysis has been applied to billow clouds; however, the critical wavelength is considered too small (of the order of a few kilometers) for this sort of instability to be the explanation for the growth of cyclonic disturbances on atmospheric fronts.
See shearing instability.

Haurwitz, B. 1941. Dynamic Meteorology. 282–292, 307–309.

INDEX
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
0
1
2
3
4
5
6
7
8
9