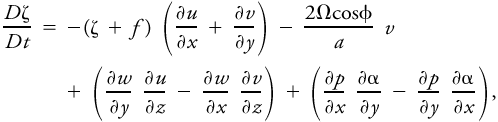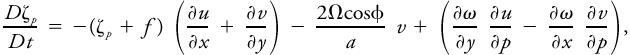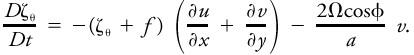Vorticity equation: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == vorticity equation == </div> <div class="definition"><div class="short_definition">A dynami...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">A dynamic equation for the rate of change of the [[vorticity]] of a [[parcel]], obtained by taking the [[curl]] of the [[vector]] equation of motion.</div><br/> <div class="paragraph">The vorticity equation takes on slightly different forms depending on whether height or [[pressure]] is taken as the vertical coordinate. With height as the vertical coordinate, and with [[friction]] terms omitted, the vertical component of the vorticity equation is <div class="display-formula"><blockquote>[[File:ams2001glos-Ve21.gif|link=|center|ams2001glos-Ve21]]</blockquote></div> where ζ is the vertical component of the [[relative vorticity]]; ''f'' the [[Coriolis parameter]]; ''u'', ''v'', and ''w'' the components of the [[wind]] velocity toward the east (''x''), north (''y''), and vertical (''z''); Ω the angular speed of the earth; ''p'' and α the air [[pressure]] and [[specific volume]], respectively; ''a'' the earth's radius; and φ the latitude. The left-hand member of the equation represents the material rate of change of the relative vorticity of an [[air parcel]]. The first term on the right describes the effect of [[horizontal divergence]]. The second term on the right is the [[Rossby parameter]] times ''v'' and represents the change in vorticity resulting from latitudinal displacement. The third term on the right, often called the vertical [[shear]], [[twisting]], or tilting term, describes the influence of a horizontal [[gradient]] of [[vertical velocity]] in transforming vorticity about a horizontal axis to that about a vertical axis. The last term represents the generation of vorticity by pressure–volume [[solenoids]]. When pressure is taken as the vertical coordinate, and all differentiations are performed on an [[isobaric surface]], the equation is simplified by the absence of the [[solenoidal]] term: <div class="display-formula"><blockquote>[[File:ams2001glos-Ve22.gif|link=|center|ams2001glos-Ve22]]</blockquote></div> where ζ<sub>''p''</sub> is the [[isobaric vorticity]] and ω = ''Dp''/''Dt'' is the material pressure change. If [[adiabatic]] processes are assumed, and [[potential temperature]] θ taken as vertical coordinate, all differentiations are performed on an [[isentropic surface]], and the vorticity equation becomes <div class="display-formula"><blockquote>[[File:ams2001glos-Ve23.gif|link=|center|ams2001glos-Ve23]]</blockquote></div></div><br/></div><div class="reference">Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 102–113. </div><br/> | <div class="definition"><div class="short_definition">A dynamic equation for the rate of change of the [[vorticity]] of a [[parcel]], obtained by taking the [[curl]] of the [[vector]] equation of motion.</div><br/> <div class="paragraph">The vorticity equation takes on slightly different forms depending on whether height or [[pressure]] is taken as the vertical coordinate. With height as the vertical coordinate, and with [[friction]] terms omitted, the vertical component of the vorticity equation is <div class="display-formula"><blockquote>[[File:ams2001glos-Ve21.gif|link=|center|ams2001glos-Ve21]]</blockquote></div> where ζ is the vertical component of the [[relative vorticity]]; ''f'' the [[Coriolis parameter]]; ''u'', ''v'', and ''w'' the components of the [[wind]] velocity toward the east (''x''), north (''y''), and vertical (''z''); Ω the angular speed of the earth; ''p'' and α the air [[pressure]] and [[specific volume]], respectively; ''a'' the earth's radius; and φ the latitude. The left-hand member of the equation represents the material rate of change of the relative vorticity of an [[air parcel]]. The first term on the right describes the effect of [[horizontal divergence]]. The second term on the right is the [[Rossby parameter]] times ''v'' and represents the change in vorticity resulting from latitudinal displacement. The third term on the right, often called the vertical [[shear]], [[twisting term|twisting]], or tilting term, describes the influence of a horizontal [[gradient]] of [[vertical velocity]] in transforming vorticity about a horizontal axis to that about a vertical axis. The last term represents the generation of vorticity by pressure–volume [[solenoids]]. When pressure is taken as the vertical coordinate, and all differentiations are performed on an [[isobaric surface]], the equation is simplified by the absence of the [[solenoidal]] term: <div class="display-formula"><blockquote>[[File:ams2001glos-Ve22.gif|link=|center|ams2001glos-Ve22]]</blockquote></div> where ζ<sub>''p''</sub> is the [[isobaric vorticity]] and ω = ''Dp''/''Dt'' is the material pressure change. If [[adiabatic]] processes are assumed, and [[potential temperature]] θ taken as vertical coordinate, all differentiations are performed on an [[isentropic surface]], and the vorticity equation becomes <div class="display-formula"><blockquote>[[File:ams2001glos-Ve23.gif|link=|center|ams2001glos-Ve23]]</blockquote></div></div><br/></div><div class="reference">Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 102–113. </div><br/> | ||
</div> | </div> | ||
Latest revision as of 17:13, 25 April 2012
vorticity equation
A dynamic equation for the rate of change of the vorticity of a parcel, obtained by taking the curl of the vector equation of motion.
The vorticity equation takes on slightly different forms depending on whether height or pressure is taken as the vertical coordinate. With height as the vertical coordinate, and with friction terms omitted, the vertical component of the vorticity equation is where ζ is the vertical component of the relative vorticity; f the Coriolis parameter; u, v, and w the components of the wind velocity toward the east (x), north (y), and vertical (z); Ω the angular speed of the earth; p and α the air pressure and specific volume, respectively; a the earth's radius; and φ the latitude. The left-hand member of the equation represents the material rate of change of the relative vorticity of an air parcel. The first term on the right describes the effect of horizontal divergence. The second term on the right is the Rossby parameter times v and represents the change in vorticity resulting from latitudinal displacement. The third term on the right, often called the vertical shear, twisting, or tilting term, describes the influence of a horizontal gradient of vertical velocity in transforming vorticity about a horizontal axis to that about a vertical axis. The last term represents the generation of vorticity by pressure–volume solenoids. When pressure is taken as the vertical coordinate, and all differentiations are performed on an isobaric surface, the equation is simplified by the absence of the solenoidal term: where ζp is the isobaric vorticity and ω = Dp/Dt is the material pressure change. If adiabatic processes are assumed, and potential temperature θ taken as vertical coordinate, all differentiations are performed on an isentropic surface, and the vorticity equation becomes
Holton, J. R. 1992. An Introduction to Dynamic Meteorology. 3d edition, Academic Press, . 102–113.