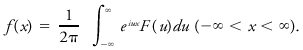Fourier transform: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == Fourier transform == </div> <div class="definition"><div class="short_definition">An analyt...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">An analytical transformation of a function ''f''(''x'') obtained (if it exists) by multiplying the function by ''e''<sup> | <div class="definition"><div class="short_definition">An analytical transformation of a function ''f''(''x'') obtained (if it exists) by multiplying the function by ''e''<sup>-''iux''</sup> and integrating over all ''x'', <div class="display-formula"><blockquote>[[File:ams2001glos-Fe14.gif|link=|center|ams2001glos-Fe14]]</blockquote></div> where ''u'' is the new [[variable]] of the transform ''F''(''u'') and ''i''<sup>2</sup> = -1.</div><br/> <div class="paragraph">If the Fourier transform of a function is known, the function itself may be recovered by use of the inversion formula: <div class="display-formula"><blockquote>[[File:ams2001glos-Fe15.gif|link=|center|ams2001glos-Fe15]]</blockquote></div> The Fourier transform has the same uses as the [[Fourier series]]: For example, the integrand F(''u'') exp (''iux'') is a solution of a given [[linear]] equation, so that the integral sum of these solutions is the most general solution of the equation. When the variable ''u'' is complex, the Fourier transform is equivalent to the [[Laplace transform]]. <br/>''See also'' [[Fourier integral]], [[spectral function]].</div><br/> </div> | ||
</div> | </div> | ||
Latest revision as of 14:15, 20 February 2012
Fourier transform
An analytical transformation of a function f(x) obtained (if it exists) by multiplying the function by e-iux and integrating over all x, where u is the new variable of the transform F(u) and i2 = -1.
If the Fourier transform of a function is known, the function itself may be recovered by use of the inversion formula: The Fourier transform has the same uses as the Fourier series: For example, the integrand F(u) exp (iux) is a solution of a given linear equation, so that the integral sum of these solutions is the most general solution of the equation. When the variable u is complex, the Fourier transform is equivalent to the Laplace transform.
See also Fourier integral, spectral function.
See also Fourier integral, spectral function.