Gradient: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == gradient == </div> #<div class="definition"><div class="short_definition">The space rate of...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
#<div class="definition"><div class="short_definition">The space rate of decrease of a function.</div><br/> <div class="paragraph">The gradient of a function in three space dimensions is the [[vector]] normal to surfaces of constant value of the function and directed toward decreasing values, with magnitude equal to the rate of decrease of the function in this direction. The gradient of a function ''f'' is denoted by | #<div class="definition"><div class="short_definition">The space rate of decrease of a function.</div><br/> <div class="paragraph">The gradient of a function in three space dimensions is the [[vector]] normal to surfaces of constant value of the function and directed toward decreasing values, with magnitude equal to the rate of decrease of the function in this direction. The gradient of a function ''f'' is denoted by -'''∇'''''f'' (without the minus sign in the older literature) and is itself a function of both space and time. The [[ascendent]] is the negative of the gradient. In [[Cartesian coordinates]], the expression for the gradient is <div class="display-formula"><blockquote>[[File:ams2001glos-Ge34.gif|link=|center|ams2001glos-Ge34]]</blockquote></div> For expressions in other coordinate systems, see Berry et al. (1945).</div><br/> </div> | ||
#<div class="definition"><div class="short_definition">Often loosely used to denote the magnitude of the gradient or ascendent (i.e., without regard to sign) of a horizontal [[pressure field]].</div><br/> </div><div class="reference">Berry, F. A., E. Bollay, and N. Beers 1945. Handbook of Meteorology. 224–225. </div><br/> | #<div class="definition"><div class="short_definition">Often loosely used to denote the magnitude of the gradient or ascendent (i.e., without regard to sign) of a horizontal [[pressure field]].</div><br/> </div><div class="reference">Berry, F. A., E. Bollay, and N. Beers 1945. Handbook of Meteorology. 224–225. </div><br/> | ||
</div> | </div> | ||
Latest revision as of 14:20, 20 February 2012
gradient[edit | edit source]
- The space rate of decrease of a function.
The gradient of a function in three space dimensions is the vector normal to surfaces of constant value of the function and directed toward decreasing values, with magnitude equal to the rate of decrease of the function in this direction. The gradient of a function f is denoted by -∇f (without the minus sign in the older literature) and is itself a function of both space and time. The ascendent is the negative of the gradient. In Cartesian coordinates, the expression for the gradient isFor expressions in other coordinate systems, see Berry et al. (1945).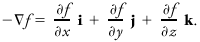
- Often loosely used to denote the magnitude of the gradient or ascendent (i.e., without regard to sign) of a horizontal pressure field.
Berry, F. A., E. Bollay, and N. Beers 1945. Handbook of Meteorology. 224–225.
