Lee wave: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == lee wave == </div> #<div class="definition"><div class="short_definition">Any [[wave distur...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
#<div class="definition"><div class="short_definition">Any [[wave disturbance]] that is caused by, and is therefore stationary with respect to, some barrier in the fluid flow.</div><br/> <div class="paragraph">Whether the [[wave]] is a [[gravity wave]], [[inertia wave]], [[barotropic wave]], etc., will depend on the structure of the fluid and the dimensions of the barrier. Most research has been devoted to the gravity lee wave ([[mountain wave]]) in the [[atmosphere]], of [[wavelength]] of order <div class="display-formula"><blockquote>[[File:ams2001glos-Le13.gif|link=|center|ams2001glos-Le13]]</blockquote></div> where ''V'' is the current speed, ''T'' the Kelvin [[temperature]], ''g'' the [[acceleration of gravity]], and γ<sub>''d''</sub> and γ the [[dry-adiabatic]] and [[environmental lapse rates]], respectively. This is the wave that is evident in [[lenticular]] or [[Moazagotl]] cloud systems and is strikingly exemplified in the [[Bishop wave]]. Dynamically, the lee wave is the sum of the [[free waves]] of the system and those wave components forced by the particular shape of the barrier. The [[disturbance]] is, in general, negligible at any distance [[upstream]] of the barrier, a result that follows from the dynamics when the system is started from rest, but a point that requires special attention when the steady-state assumption is made. The term lee wave is also applied loosely to nonwave disturbances in the lee of obstacles, such as the [[rotor cloud]].</div><br/> </div> | #<div class="definition"><div class="short_definition">Any [[wave disturbance]] that is caused by, and is therefore stationary with respect to, some barrier in the fluid flow.</div><br/> <div class="paragraph">Whether the [[wave]] is a [[gravity wave]], [[inertia wave]], [[barotropic wave]], etc., will depend on the structure of the fluid and the dimensions of the barrier. Most research has been devoted to the gravity lee wave ([[mountain wave]]) in the [[atmosphere]], of [[wavelength]] of order <div class="display-formula"><blockquote>[[File:ams2001glos-Le13.gif|link=|center|ams2001glos-Le13]]</blockquote></div> where ''V'' is the current speed, ''T'' the Kelvin [[temperature]], ''g'' the [[acceleration of gravity]], and γ<sub>''d''</sub> and γ the [[dry-adiabatic lapse rate|dry-adiabatic]] and [[environmental lapse rates]], respectively. This is the wave that is evident in [[lenticularis|lenticular]] or [[Moazagotl]] cloud systems and is strikingly exemplified in the [[Bishop wave]]. Dynamically, the lee wave is the sum of the [[free waves]] of the system and those wave components forced by the particular shape of the barrier. The [[disturbance]] is, in general, negligible at any distance [[upstream]] of the barrier, a result that follows from the dynamics when the system is started from rest, but a point that requires special attention when the steady-state assumption is made. The term lee wave is also applied loosely to nonwave disturbances in the lee of obstacles, such as the [[rotor cloud]].</div><br/> </div> | ||
#<div class="definition"><div class="short_definition">A [[mountain wave]] occurring to the lee of a mountain or mountain barrier.</div><br/> <div class="paragraph">These waves can become visible in the form of [[lenticular]] or trapped lee-wave clouds.</div><br/> </div><div class="reference">Eliassen, A., and E. Kleinschmidt 1957. Dynamic Meteorology. Handbuch der Geophysik. Vol. XLVIII, . 59– 64. </div><br/> | #<div class="definition"><div class="short_definition">A [[mountain wave]] occurring to the lee of a mountain or mountain barrier.</div><br/> <div class="paragraph">These waves can become visible in the form of [[lenticularis|lenticular]] or trapped lee-wave clouds.</div><br/> </div><div class="reference">Eliassen, A., and E. Kleinschmidt 1957. Dynamic Meteorology. Handbuch der Geophysik. Vol. XLVIII, . 59– 64. </div><br/> | ||
</div> | </div> | ||
Latest revision as of 16:19, 25 April 2012
lee wave
- Any wave disturbance that is caused by, and is therefore stationary with respect to, some barrier in the fluid flow.
Whether the wave is a gravity wave, inertia wave, barotropic wave, etc., will depend on the structure of the fluid and the dimensions of the barrier. Most research has been devoted to the gravity lee wave (mountain wave) in the atmosphere, of wavelength of orderwhere V is the current speed, T the Kelvin temperature, g the acceleration of gravity, and γd and γ the dry-adiabatic and environmental lapse rates, respectively. This is the wave that is evident in lenticular or Moazagotl cloud systems and is strikingly exemplified in the Bishop wave. Dynamically, the lee wave is the sum of the free waves of the system and those wave components forced by the particular shape of the barrier. The disturbance is, in general, negligible at any distance upstream of the barrier, a result that follows from the dynamics when the system is started from rest, but a point that requires special attention when the steady-state assumption is made. The term lee wave is also applied loosely to nonwave disturbances in the lee of obstacles, such as the rotor cloud.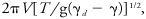
- A mountain wave occurring to the lee of a mountain or mountain barrier.
These waves can become visible in the form of lenticular or trapped lee-wave clouds.
Eliassen, A., and E. Kleinschmidt 1957. Dynamic Meteorology. Handbuch der Geophysik. Vol. XLVIII, . 59– 64.
