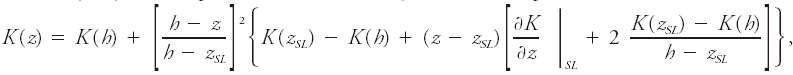O'brien cubic polynomial: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == O'Brien cubic polynomial == </div> <div class="definition"><div class="short_definition">An...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">An approximation for the [[eddy diffusivity]] ''K'' as a function of height ''z'' in a [[boundary layer]] of depth ''h'' with [[surface layer]] (SL) of depth ''z''<sub>''SL''</sub>: <div class="display-formula"><blockquote>[[File:ams2001glos-Oe1.gif|link=|center|ams2001glos-Oe1]]</blockquote></div> where the tunable parameters in the equation are eddy diffusivities at the top of the surface layer and at the top of the boundary layer, ''K''(''z''<sub>''SL''</sub>) and ''K''(''h''), respectively, the heights of those two layers, and the [[gradient]] of eddy diffusivity at the top of the surface layer ∂''K''/∂''z''.</div><br/> <div class="paragraph">Above the top of the boundary layer the eddy diffusivity is assumed to be constant at ''K''(''h''), while at the surface it is assumed to be zero. <br/>''See'' [[K-theory]], [[gradient transport theory]], [[first-order closure]], [[closure assumptions]].</div><br/> </div><div class="reference">O'Brien, J. J. 1970. A note on the vertical structure of the eddy exchange coefficient in the planetary boundary layer. J. Atmos. Sci.. 27. 1213–1215. </div><br/> | <div class="definition"><div class="short_definition">An approximation for the [[eddy diffusivity]] ''K'' as a function of height ''z'' in a [[boundary layer]] of depth ''h'' with [[surface layer]] (SL) of depth ''z''<sub>''SL''</sub>: <div class="display-formula"><blockquote>[[File:ams2001glos-Oe1.gif|link=|center|ams2001glos-Oe1]]</blockquote></div> where the tunable parameters in the equation are eddy diffusivities at the top of the surface layer and at the top of the boundary layer, ''K''(''z''<sub>''SL''</sub>) and ''K''(''h''), respectively, the heights of those two layers, and the [[gradient]] of eddy diffusivity at the top of the surface layer ∂''K''/∂''z''.</div><br/> <div class="paragraph">Above the top of the boundary layer the eddy diffusivity is assumed to be constant at ''K''(''h''), while at the surface it is assumed to be zero. <br/>''See'' [[K-theory]], [[gradient transport theory]], [[first-order closure|first-order closure]], [[closure assumptions]].</div><br/> </div><div class="reference">O'Brien, J. J. 1970. A note on the vertical structure of the eddy exchange coefficient in the planetary boundary layer. J. Atmos. Sci.. 27. 1213–1215. </div><br/> | ||
</div> | </div> | ||
Latest revision as of 16:31, 25 April 2012
O'Brien cubic polynomial[edit | edit source]
An approximation for the eddy diffusivity K as a function of height z in a boundary layer of depth h with surface layer (SL) of depth zSL: where the tunable parameters in the equation are eddy diffusivities at the top of the surface layer and at the top of the boundary layer, K(zSL) and K(h), respectively, the heights of those two layers, and the gradient of eddy diffusivity at the top of the surface layer ∂K/∂z.
Above the top of the boundary layer the eddy diffusivity is assumed to be constant at K(h), while at the surface it is assumed to be zero.
See K-theory, gradient transport theory, first-order closure, closure assumptions.
See K-theory, gradient transport theory, first-order closure, closure assumptions.
O'Brien, J. J. 1970. A note on the vertical structure of the eddy exchange coefficient in the planetary boundary layer. J. Atmos. Sci.. 27. 1213–1215.