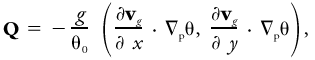Q vector: Difference between revisions
From Glossary of Meteorology
imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == Q vector == </div> <div class="definition"><div class="short_definition">A horizontal [[vec...") |
imported>Perlwikibot No edit summary |
||
| Line 9: | Line 9: | ||
</div> | </div> | ||
<div class="definition"><div class="short_definition">A horizontal [[vector]], arising in [[quasigeostrophic]] and [[semigeostrophic theory]], the [[divergence]] of which appears on the right-hand side of the [[omega equation]].</div><br/> <div class="paragraph">In the context of [[''f''-plane]] (i.e., the [[Coriolis parameter]] ''f'' is assumed constant) quasigeostrophic theory, the '''Q''' vector is defined as <div class="display-formula"><blockquote>[[File:ams2001glos-Qe1.gif|link=|center|ams2001glos-Qe1]] </blockquote></div> where ''g'' is the [[acceleration of gravity]], θ<sub>0</sub> a constant reference value of the [[potential temperature]], '''v'''<sub>''g''</sub> the horizontal [[geostrophic wind]], '''∇'''<sub>p</sub> the horizontal [[gradient]] operator on a [[constant-pressure surface]], and θ the potential temperature. In the context of ''f''-plane semigeostrophic theory, the definition of the '''Q''' [[vector]] is identical except that the physical coordinates (''x, y'') are replaced by the [[geostrophic coordinates]] (''X, Y''). The '''Q''' vector tends to point in the direction of rising air. If '''Q''' points toward warm air, the [[geostrophic flow]] is [[frontogenetic]]. If '''Q''' points toward cold air, the geostrophic flow is [[frontolytic]].</div><br/> </div> | <div class="definition"><div class="short_definition">A horizontal [[vector]], arising in [[quasigeostrophic theory|quasigeostrophic]] and [[semigeostrophic theory]], the [[divergence]] of which appears on the right-hand side of the [[omega equation]].</div><br/> <div class="paragraph">In the context of [[''f''-plane]] (i.e., the [[Coriolis parameter]] ''f'' is assumed constant) quasigeostrophic theory, the '''Q''' vector is defined as <div class="display-formula"><blockquote>[[File:ams2001glos-Qe1.gif|link=|center|ams2001glos-Qe1]] </blockquote></div> where ''g'' is the [[acceleration of gravity]], θ<sub>0</sub> a constant reference value of the [[potential temperature]], '''v'''<sub>''g''</sub> the horizontal [[geostrophic wind]], '''∇'''<sub>p</sub> the horizontal [[gradient]] operator on a [[constant-pressure surface|constant-pressure surface]], and θ the potential temperature. In the context of ''f''-plane semigeostrophic theory, the definition of the '''Q''' [[vector]] is identical except that the physical coordinates (''x, y'') are replaced by the [[geostrophic coordinates]] (''X, Y''). The '''Q''' vector tends to point in the direction of rising air. If '''Q''' points toward warm air, the [[geostrophic flow]] is [[frontogenesis|frontogenetic]]. If '''Q''' points toward cold air, the geostrophic flow is [[frontolytic]].</div><br/> </div> | ||
</div> | </div> | ||
Latest revision as of 16:41, 25 April 2012
Q vector
A horizontal vector, arising in quasigeostrophic and semigeostrophic theory, the divergence of which appears on the right-hand side of the omega equation.
In the context of ''f''-plane (i.e., the Coriolis parameter f is assumed constant) quasigeostrophic theory, the Q vector is defined as where g is the acceleration of gravity, θ0 a constant reference value of the potential temperature, vg the horizontal geostrophic wind, ∇p the horizontal gradient operator on a constant-pressure surface, and θ the potential temperature. In the context of f-plane semigeostrophic theory, the definition of the Q vector is identical except that the physical coordinates (x, y) are replaced by the geostrophic coordinates (X, Y). The Q vector tends to point in the direction of rising air. If Q points toward warm air, the geostrophic flow is frontogenetic. If Q points toward cold air, the geostrophic flow is frontolytic.