Gradient transport theory

From Glossary of Meteorology
Revision as of 17:09, 26 January 2012 by imported>Perlwikibot (Created page with " {{TermHeader}} {{TermSearch}} <div class="termentry"> <div class="term"> == gradient transport theory == </div> <div class="definition"><div class="short_definition">A...")
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)



gradient transport theory

A first-order turbulence closure approximation that assumes that turbulent fluxes of any variable flow down the local gradient of that mean variable; analogous to molecular transport.

This local turbulence closure approach assumes that turbulence consists of only small eddies, causing diffusion-like transport. An example is
ams2001glos-Ge36
where the vertical kinematic flux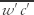
ams2001glos-Gex03
of a pollutant is modeled as being equal to an eddy thermal diffusivity K times the vertical gradient of mean concentration
ams2001glos-Gex04
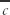. This theory is
also called K- theory or eddy-viscosity theory.
Compare higher-order closure, nonlocal closure, transilient turbulence theory.


Retrieved from "https://glossarystaging.ametsoc.net/w/index.php?title=Gradient_transport_theory&oldid=18749"
Powered by MediaWiki
Powered by WikiTeq
Powered by Semantic MediaWiki
Copyright 2024 American Meteorological Society (AMS). For permission to reuse any portion of this work, please contact permissions@ametsoc.org. Any use of material in this work that is determined to be “fair use” under Section 107 of the U.S. Copyright Act (17 U.S. Code § 107) or that satisfies the conditions specified in Section 108 of the U.S.Copyright Act (17 USC § 108) does not require AMS’s permission. Republication, systematic reproduction, posting in electronic form, such as on a website or in a searchable database, or other uses of this material, except as exempted by the above statement, require written permission or a license from AMS. Additional details are provided in the AMS Copyright Policy statement.